
Iniciando el Club de Matemáticas
El Sr. Power era un profesor de matemáticas al que le gustaba que los estudiantes participaran. Habló con algunos estudiantes y les preguntó si estarían interesados en formar un club extracurricular de Matemáticas. Los estudiantes harían presentaciones mensuales en el club. Pueden presentar cualquier cosa siempre que esté relacionada con las Matemáticas de una forma u otra, y más adelante el club podría agregar otras actividades. Sugirió que cualquier estudiante de la escuela pudiera participar. Preguntó si había alguien que quisiera iniciar el club. Dos estudiantes llamados Kirsten y Jonathan aceptaron tomar la iniciativa. Kirsten y Jonathan tenían calificaciones promedio pero eran extremadamente sociables. Les gustaba hablar con todos en la escuela. Se reunieron con varios estudiantes y hablaron sobre la idea del Sr. Power. También consiguieron firmas de los alumnos que querían sumarse. Algunos de los estudiantes firmaron porque estaban realmente interesados. También hubo otros que firmaron simplemente porque no tenían nada que perder. No hubo tarifas ni compromisos firmes y rápidos.
Después de hablar con sus compañeros de clase y obtener estas firmas, Kirsten y Jonathan se reunieron con el Sr. Power y le dijeron que unos 50 estudiantes querían unirse, en su mayoría de los grados 11 y 12, y algunos del grado 10. El Sr. Power no estaba contento de que No había estudiantes de noveno grado, pero lo dejó pasar pensando que tal vez se les preguntara más tarde por un anuncio de su maestro de Matemáticas.
Camisetas del club de matemáticas
Kirsten y Jonathan también le dijeron que los estudiantes sugirieron que hicieran camisetas para los que se unieran al club. De hecho, dieron la impresión de que las camisetas podrían aumentar el interés de los estudiantes. También querían saber si la escuela podría contribuir con estas camisetas y cuánto. El Sr. Power lo pensó, habló con el director y luego dijo que la escuela contribuiría con el 60% del costo de las camisas y que los estudiantes tendrían que compartir el 40% restante. Esto estaba condicionado a la aprobación del logotipo basado en Matemáticas que se imprimiría en las camisetas. Alguien del grupo tendría que mostrar el diseño y hacerle una presentación a él y al Director para que este fondo sea aprobado. También les advirtió que tendrían que trabajar en un buen concepto matemático y no simplemente en algo como dos más tres es igual a cinco.
Kirsten y Jonathan convocaron una reunión del club de Matemáticas para discutir cualquier sugerencia para el diseño del logotipo. Al principio, hubo un completo silencio, pero luego vino la primera sugerencia. Era dibujar un círculo con la escritura πr2 en el medio. Otro era dibujar formas con diferente número de lados. Estas ideas pueden no haber sido muy interesantes o muy atractivas, pero iniciaron la conversación.

Diseño de logotipos y teorema de Pitágoras
Luego, un estudiante sugirió un triángulo de ángulo recto para la prueba del teorema de Pitágoras. Usaría cuatro colores diferentes: uno para el triángulo de ángulo recto y un color diferente para cada uno de los cuadrados que podrían dibujarse desde los tres lados del triángulo. Kirsten y Jonathan se dieron cuenta y dijeron que estaban pensando en esta idea pero de una manera más avanzada. Lo llamaron un triple pitagórico. Un triple pitagórico es un triángulo de ángulo recto con todos sus lados números enteros. El primer triple tiene los lados 3, 4, 5 porque 32 + 42 = 52. El siguiente triple es 5, 12, 13 pero daría un triángulo de una forma extraña. Además, la dirección de la escuela era 345 Triangle Park. Solicitaron esta idea (Fig. 4.1).
Conectando trigonometría y geometría
A todos les gustó esta idea, pero un estudiante levantó la mano y dijo: “Esto puede pasar, pero debemos mejorarlo para asegurarnos de obtener el dinero”. En nuestra clase de álgebra, nuestro maestro de matemáticas nos retó a conectar la aritmética, la geometría y el álgebra. Sara dio la solución para eso. Sara, ¿puedes pensar en algo que conecte esta figura geométrica con otra materia de Matemáticas?”
Sara: Johnny y yo estuvimos hablando sobre el teorema de Pitágoras el otro día mientras estudiábamos Trigonometría. Aquellos de ustedes en los últimos años deben haber estudiado las identidades trigonométricas y sabrán que algunas de ellas se derivan de sin2 x + cos2 x = 1.
Uno de los estudiantes dijo: sí, recuerdo dos identidades basadas en sin2 x + cos2 x = 1. Recuerdo sec2 x = 1 + tan2 x y cosec2 x = 1 + cot2x.
Sara: Sin2 x + Cos2 x =1 es una reformulación trigonométrica del teorema de Pitágoras.
Muchos estudiantes dijeron cómo habían usado el teorema de Pitágoras para probar esta identidad.
Kirsten y Jonathan acordaron que esta era una buena idea para conectar Geometría y Trigonometría, pero aún querían usar la idea de la terna pitagórica.
Sara levantó la mano y dijo: Acabo de verificar en mi calculadora que sin 37° = 0.6018 que es aproximadamente 3/5 y cos 37° = 0.7986 que es aproximadamente 4/5. Eso significa que un ángulo de la primera terna pitagórica con los lados 3 y 4 será de 37°. La hipotenusa será 5. Entonces, ¿qué tal si mantenemos el mismo diseño pero con algo de escritura? Fue a la pizarra y escribió algunas cosas, y la imagen final se veía así (Fig. 4.2).
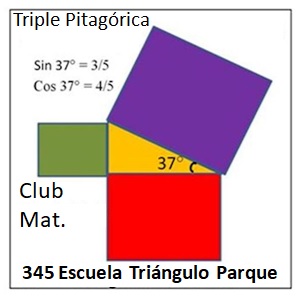
Kirsten y Jonathan pidieron una votación sobre este diseño. Se aprobó rápida y unánimemente.
Kirsten: Es genial que tengamos un diseño, pero tengo dos problemas más.
Jonatán: ¿Qué son?
Kirsten: La primera preocupación es que una imagen con el triángulo de lados 3, 4 y 5 centímetros será demasiado pequeña y no se verá bien en una camiseta.
Un estudiante gritó que el tamaño podría ser de 3, 4 y 5 pulgadas.
Kirsten sonrió y dijo: Gracias. Eso resolverá este problema.
Jonathan: Kirsten dijiste que tenías dos preocupaciones.
¿Quién hará la presentación al director?
Kirsten: Sí, ¿quién hará la presentación al Sr. Power y al director?
Muchos estudiantes señalaron a Sara.
Sara: Kirsten, tú y Jonathan hicieron todo el trabajo. Deberías hacer la presentación. Si quieres que te acompañe, estaré encantado de hacerlo.
Kirsten: ¿Qué piensan todos de esta idea?
Ellos lo amaron.
Kirsten y Jonathan fueron a una tienda de camisetas local para pedir un presupuesto de 50 camisetas. Dijeron que el costo total de 50 camisetas era de $600 más impuestos, pero como descuento, la tienda podía pagar los impuestos.
Kirsten, Johnathan y Sara impresionaron a los maestros con su presentación del diseño y los conceptos matemáticos que lo sustentan. La escuela acordó pagar el 60% del costo de las camisetas. Eso significaba que de los $600, la escuela pagaría $360 y los estudiantes recibirían los $240 restantes. Entonces las camisetas costarían sólo $240/50 o $4.80 por estudiante. Entonces se inició el Club de Matemáticas.
Desafío
Sara quería saber cuántos regalos recibiría en su cumpleaños. Su mamá le dio esta respuesta directa: 4 sin2 x + 2 – 2 tan2 x + 4 cos2x + 2 sec2 x. Sara dijo: “gracias mamá”.
Supongo que Sara lo descubrió. ¿Puede?
Solución: : Objetivo: Simplificar 4 sin2 x + 2 – 2 tan2 x + 4 cos2x + 2 sec2x
Del teorema de Pitágoras sin2 x + cos2x = 1
Dividiendo ambos lados por cos2x, se obtiene tan2 x + 1 = sec2x o sec2x = 1+ tan2 x.
Ahora, 4 sin2 x + 2 – 2 tan2 x + 4 cos2x + 2 sec2x = 4(sin2 x + cos2x) +2 – tan2 x +2(1+ tan2 x) = 4 porque los términos restantes se cancelan.
Así que debería recibir 4 regalos en su cumpleaños. A su madre le gusta complicar las cosas.