
Introducción a las ecuaciones cuadráticas
Sra. Clementine: Kwong, ahora que ha presentado el concepto de una relación cuadrática en su proyecto de feria de ciencias, tal vez toda la clase debería aprender sobre él. Iba a enseñarlo más tarde, pero este parece ser un buen momento. Debido a que la clase ya participó en esta encuesta, es posible que todos también puedan hablar sobre ella. Sara, ¿querrías darle a la clase una idea básica de una relación cuadrática?
Sara: Puedo intentarlo pero solo la idea muy básica.
Sra. Clementine: Por favor, pase al frente entonces.
Sara dijo: “Hola a todos. Como todos ustedes, todavía tengo que aprender sobre esta área. ¿Recuerdan cuando aprendimos sobre la relación lineal y = a + bx? Por ejemplo, cuando camina, su posición depende de dónde empezaste más qué tan rápido caminas multiplicado por cuánto tiempo has caminado. Creo que todos en la clase recuerdan eso.
No siempre es tan simple. No todas las relaciones son lineales. Kwong te mostró un gráfico curvo. Supongamos que los estudiantes pueden hacer un buen uso de los teléfonos para aprender. Tal vez al usar los teléfonos inteligentes, puedan obtener más recursos para aprender o tal vez explicarse cosas entre ellos. Entonces, esperaría un efecto positivo del uso del teléfono celular en lo académico. Pero entonces, alguien podría decir que el tiempo que pasas en el teléfono se está quitando de tu tiempo de estudio. Si es así, el uso del teléfono disminuirá su tiempo de estudio o la cantidad de atención que puede prestar a sus estudios. El uso excesivo del teléfono tendrá resultados negativos, como señaló la Sra. Clementine a la clase. Con una ecuación cuadrática podrías explicar ambos efectos juntos. Tendrá la forma general de y = ax2 + bx + c. En el ejemplo de Kwong, era y = -2,4x2 +9,6x + 76,8. Supongo que la Sra. Clementine nos enseñará más al respecto.
Sra. Clementine: Todos, saben que una función cuadrática se escribe como y = ax2 + bx + c. Por lo general, se le pedirá que determine los valores de x cuando
ax2 + bx + c = 0.
Resolviendo las ecuaciones cuadráticas
Puedo pensar en cuatro formas diferentes de resolver la ecuación: graficar, factorizar, completar los cuadrados y usar la fórmula cuadrática. Cada método será presentado por un grupo diferente de estudiantes. La siguiente clase será sobre los dos primeros métodos, y la siguiente clase será sobre los métodos tercero y cuarto. Después de esto, un grupo presentará el concepto de vértice. Los estudiantes restantes vendrán preparados para informar sobre las relaciones cuadráticas en algo de su experiencia o interés. Publicaré la lista de estudiantes y sus temas.
———————-Siguiente clase———————-
Sra. Clementine: Tengamos la presentación del primer grupo. Kathy: Usamos la ecuación de Kwong para el rendimiento académico frente al uso de teléfonos inteligentes, como se muestra en esta imagen. Debido a que queríamos resolver la ecuación -2.4x2 +9.6x + 76.8 = 0, trazamos un gráfico continuo sobre más valores y sobre un dominio de x más grande que el que Kwong nos había mostrado (Fig. 7.3). Luego buscamos los valores de x donde y = 0. La gráfica mostró que y=0 cuando x = -4 o x = +8. Usar el teléfono durante menos 4 horas al día no tenía ningún sentido. Las marcas negativas en los gráficos tampoco tenían ningún sentido para nosotros. Por lo tanto, concluimos que es posible obtener un promedio de calificación de cero si usa el teléfono durante 8 horas por día. ¿Cuándo comes, duermes, juegas y estudias si usas el teléfono durante 8 horas al día?
Sra. Clementine: Gracias por una presentación clara. El grupo 2 es el siguiente.
Joe: También resolvimos la ecuación de la función cuadrática de Kwong pero por factorización. La ecuación cuadrática era -2,4x2 + 9,6x + 76,8 = 0. Al principio, no sabíamos cómo factorizar esta ecuación con todos los decimales, pero alguien nos ayudó. Gracias Sara. Sara nos dijo que el problema se vuelve muy fácil si dividimos ambos lados de la ecuación por -2.4. Al hacerlo, la ecuación se convirtió en x2 – 4x -32 = 0. Ahora, 32 = 4 × 8. También 8 – 4 = 4, y 4 es el término medio de la izquierda. Por lo tanto, la ecuación factorizada se convierte en (x-8) (x+4) = 0. Eso significa que
x – 8 = 0 lo que da x = 8 o x + 4 = 0 lo que da x = -4. Así que obtuvimos la misma respuesta que el primer grupo pero no pensamos mucho en el significado de los valores negativos de x.
Sra. Clementine: Muy bien. Tienes la misma respuesta para la misma ecuación. Te daré una hoja con 6 ecuaciones diferentes. Todos tienen que hacerlas por los dos métodos presentados por Kathy y Joe, y entregar las respuestas en la siguiente clase.
——————-Siguiente clase——————-
Los grupos 3 y 4 presentados en la siguiente clase.
Jonathan: Leemos en el libro que, al completar el cuadrado, la idea es reorganizar los términos de la ecuación cuadrática para que solo tenga un término con x y el otro término sea una constante. Al igual que el otro grupo, también dividimos la ecuación de Kwong por -2,4. Eso lo hizo mucho más fácil. Entonces teníamos x2 – 4x -32 = 0. Así que empezamos a pensar en trabajar con x2 – 4x para formar un término cuadrado.
Dijimos que (x – 2)2 = x2 – 4x + 4. Por lo tanto, x2 – 4x = (x -2)2 – 4.
Por lo tanto, reescribimos x2 – 4x -32 = 0 como (x – 2)2 = 32 + 4 = 36.
Esto nos dio x -2 = ±√36 o x – 2 = ± 6. Eso nos dio x = -4 o +8. La misma respuesta que los otros grupos.
Sra. Clementine: Muy bien. Obtuviste la misma respuesta que los demás. Ahora, el grupo 4 presentará.
Sara: Se suponía que debíamos derivar la fórmula generalizada para resolver ecuaciones cuadráticas. Nuestro grupo usó el mismo método que el grupo 3: completar el cuadrado.
La ecuación general es ax2 + bx + c = 0. Al igual que los otros grupos, dividimos ambos lados por a, para obtener: x2 /a + xb/a + c/a = 0 o x2 /a + xb/a = – c/a.
Luego completamos el cuadrado sumando (b/2a)2 a ambos lados.
Esto nos dio x2 /a + xb/a + (b/2a)2 = – c/a + (b/2a)2 que es lo mismo que:
(x + b/2a)2 = – c/a+(b/2a)2.
Sacando raíces cuadradas a ambos lados obtenemos:
x + b/2a = ±√(- c/a+(b/2a))2 = ±(√(b2-4ac))/2a
Eso nos dio x = (-b ± (√(b2-4ac)))/2a
En este método, simplemente puede escribir los valores de a, b y c y obtener los valores de x cuando y = 0.
La ecuación de Kwong es -2.4x2 + 9.6x + 76.8=0. Usamos: a = -2.4, b = 9.6 y c = 76.8 y obtuvimos la respuesta x = 2 ± 6. Sorpresa, sorpresa. Esta es la misma respuesta que todos los demás.
Sra. Clementine: Muy bien. Sara, hiciste que esta derivación pareciera muy simple.
Carmen levantó las manos: ¿Qué sucede cuando b2 – 4ac es negativo?
Sra. Clementine: Trataremos este tema en otra clase. Espera hasta entonces.
Bien clase, recuerden la hoja que les di con 6 ecuaciones diferentes en la última clase. Todos tienen que resolverlos por los métodos mostrados por Jonathan y Sara, y entregar las respuestas en la próxima clase.
Vértice
Sra. Clementine: La presentación del Grupo 5 comenzará ahora.
Jun: Soy Jun y hablaré en nombre del grupo 5. Todos vieron el emocionante gráfico de Kwong que se ajustaba a la ecuación y = -2.4x2 + 9.6x + 76.8.
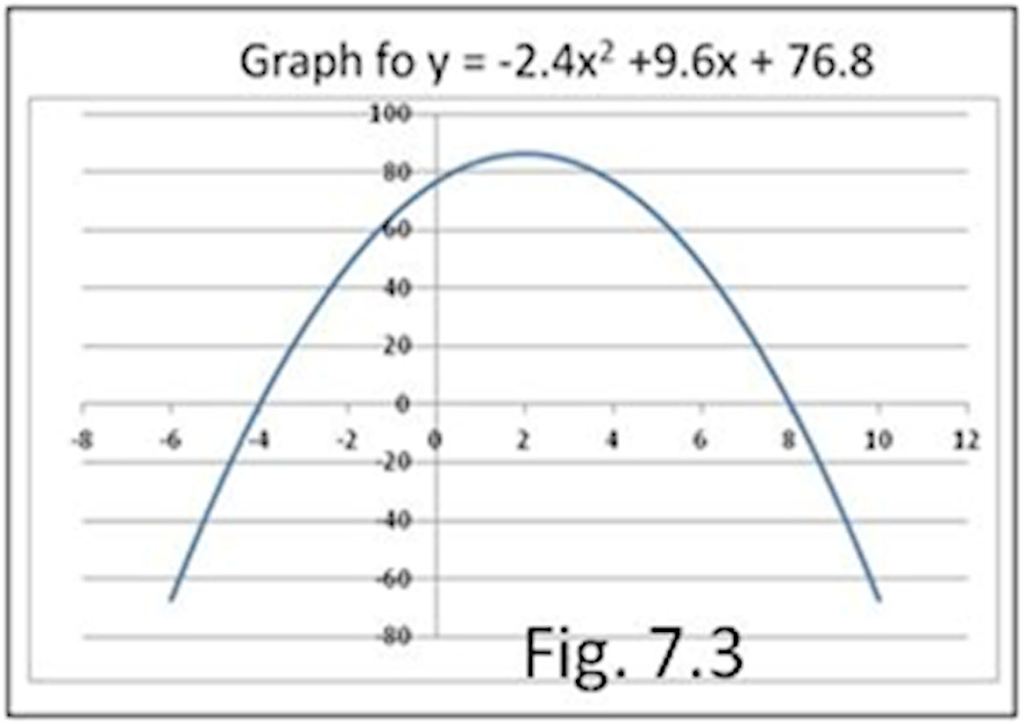
Todos resolvieron x cuando y = -2.4x2 + 9.6x + 76.8 = 0.
Sé que no quiero obtener un promedio de calificaciones de cero, que es y aquí. Quiero sacar la mejor nota que pueda. Así que basta de resolver y = 0 (lo dijo de manera desafiante).
El grupo 1 nos dio una gráfica en la que el valor de y aumenta primero y luego comienza a disminuir. En este gráfico, hay un valor de x en el que no hay aumento ni disminución en y. Esto se llama el vértice.
En el gráfico, este pico ocurre en x = 2. Ahora, si x = 2, el valor de y se convierte en -2,4 × 22 + 9,6 × 2 + 76,8, que es 86,4. Entonces decimos que el vértice está en x = 2 y y = 86.4 o en 2, y = 86.4. Hay otra manera de hacer esto. Para y = ax2 + bx + c, la pendiente de la gráfica es 2ax + b. En el vértice, la pendiente que es 2ax + b = 0. Esto significa que el vértice está en x = -b/2a. Hicimos la pregunta de esta manera y obtuvimos el valor de x en -9.6/(-2.4×2) que es 2. De esto también obtenemos el valor de y en 86.4. Entonces, el gráfico de Kwong muestra que para obtener los mejores resultados, use el teléfono durante 2 horas al día y mejore su promedio de calificaciones en casi un 10 %. Así se hace Kwong.
Sra. Clementine: Gracias por la animada presentación, Jun. ¿Recuerdas haber hablado sobre los vértices en geometría? Un vértice es un punto donde se encuentran dos rectas. De la misma manera, para una parábola el vértice es un punto donde se encuentran la subida y la bajada. Podría ser cuando ocurrirá un valor máximo o mínimo. Esta vez tenías una parábola en la que tenías un máximo. También puede obtener una parábola que inicialmente disminuye y luego comienza a aumentar. En ese caso, el vértice de esa parábola será el mínimo de la curva. Entonces, el concepto de vértice se puede usar para obtener máximos o mínimos.
Experiencia e interés de los estudiantes.
Bien, ahora tendremos ejemplos de relaciones cuadráticas a partir de la experiencia y los intereses de las personas. Por favor, vaya uno por uno en el mismo orden en que le asigné este tema.
Ashley: Soy la capitana del equipo de porristas de la escuela. Hay dos situaciones en las que caben las cuadráticas. La primera es algo así como la ecuación de Kwong. Los jueces otorgan puntajes más altos si comienzas con una ovación fácil, haces que la siguiente sea más difícil y sigues haciéndolo con tantas ovaciones como puedas. Aumentar los aplausos le otorga puntajes adicionales, pero cada aplauso adicional disminuye el rendimiento general del equipo para todos los aplausos. Esto puede deberse a que los miembros del equipo tienen dificultades para aprender demasiados aplausos o porque hay limitaciones de tiempo. Así que esto daría una relación cuadrática entre las puntuaciones y el número de aplausos. Mi amiga Kim te dirá la otra.
Kim: Hacemos un lanzamiento de canasta. Lanzamos a una niña pequeña al aire y luego la atrapamos entre todos. Si tiramos un poquito, todos abuchean. Si lanzamos muy rápido, tenemos miedo de que la cabeza de esa niña golpee el techo que tiene solo 12 metros de altura. Entonces, tengo que averiguar qué tan rápido lanzarla para que su cabeza alcance solo una altura de 11 metros para estar a salvo. Sara me dijo que esto también sería un problema de una relación cuadrática.
Dino: A mi mamá le encanta la jardinería. En una hilera de 20 metros de largo, tiene 20 plantas que le dan 1000 tomates, que son 50 tomates por planta. Discutimos que podría obtener más tomates si tuviera más plantas en la misma hilera de 20 metros. Preguntamos a un invernadero y nos dijeron que por cada planta que agreguemos, el rendimiento de cada planta disminuirá en un tomate. Creo que este también es un problema cuadrático en el que tengo que encontrar el vértice.
Tom: Esto es algo que sucedió en la tienda de mi papá. Entró una señora con un retrato con una relación de alto a ancho de 4/3. Quería ampliar la imagen a 192 pulgadas cuadradas y quería saber cuál sería la altura y el ancho de la imagen ampliada. Mi papá es muy inteligente y me dijo que lo descubrió usando una ecuación cuadrática.
Jorge: Juego baloncesto pero no soy muy alto. Necesito saltar para clavar la pelota de modo que mis pies estén a 2.5 pies del suelo. El entrenador me dijo que su profesor de kinesiología le enseñó la ecuación para saltar a la altura de 16t2 -12t donde t es el tiempo en segundos que estoy en el aire. ¿Cuánto tiempo tendré que estar en el aire para poder encestar?
Sra. Clementine: Genial. Así que ahora sabes cómo surgen los problemas verbales relacionados con las ecuaciones cuadráticas. Hay muchos de ellos en su libro. Tu tarea asignada es hacer seis de ellas antes de la próxima clase.
Desafío
El problema de Kim: Hacemos un lanzamiento de canasta. Lanzamos a una niña pequeña al aire y luego la atrapamos entre todos. Si tiramos un poquito, todos abuchean. Si lanzamos muy rápido, tenemos miedo de que la cabeza de esa niña golpee el techo que tiene solo 12 metros de altura. Entonces, tengo que averiguar qué tan rápido lanzarla para que su cabeza alcance solo una altura de 11 metros para estar a salvo. Sara me dijo que esto también sería un problema de una relación cuadrática.
El problema de Kim se puede dividir en dos partes. La primera parte se refiere a la cantidad de tiempo que le tomará a la animadora alcanzar la altura de 11 m. La segunda parte es sobre qué tan rápido lanzarla. Ambos son más fáciles de comprender preguntando cuánto tiempo le llevará llegar al suelo después de caer desde una altura de 11 m. Entonces escribiremos la relación.
Distancia = ut + at2/2
Aquí la velocidad inicial u = 0 porque cuando la niña lanzada llega a la cima, su velocidad debe ser cero porque no se mueve hacia arriba o hacia abajo en ese momento. Escribiendo a = aceleración debida a la gravedad terrestre que es 9.81 m/seg2
Entonces 11 = 0 + 9,81 t2/2 o t2/2 = 11/9,81 o t2 = 22/9,81 seg2 = 2,2425 seg2 o t = 1,4975 seg.
La velocidad v con el movimiento hacia abajo aumentará por la relación
v = u + at o v = 0 + 9,81 x 1,4975 m/s = 14,6908 m/s.
Para verificar que esta es la respuesta correcta, escribamos la relación para que la niña sea lanzada con esta velocidad inicial, pero tenga en cuenta que el movimiento de la niña ahora se desacelerará y, por lo tanto, usará el valor negativo de a
Distancia = ut + at2/2 o
Distancia = 14,6908 m/seg x 1,4975 seg – (9,81 m/seg2 x (1,4975 seg)2 )/2 o
Que es 22 – 11 = 11 metros – la altura que Kim quiere que alcance la niña.
El problema de Dino: a mi mamá le encanta la jardinería. En una hilera de 20 metros de largo, tiene 20 plantas que le dan 1000 tomates, que son 50 tomates por planta. Discutimos que podría obtener más tomates si tuviera más plantas en la misma hilera de 20 metros. Preguntamos a un invernadero y nos dijeron que el rendimiento de cada planta disminuirá en un tomate por cada planta que agreguemos. Creo que este también es un problema cuadrático en el que tengo que encontrar el vértice.
Supongamos que la mamá de Dino agrega x plantas. Entonces ella tendrá 20 + x plantas. El rendimiento de cada planta era de 50 tomates por planta pero ahora disminuirá. Cada planta agregada disminuirá el rendimiento en un tomate por planta o el rendimiento será 50 – x.
Así rendimiento (y) = (20 + x) x (50-x) = 1000 + 50x – 20x -x2
y = – x2 + 30x+ 1000
Jun dijo en la clase que vértice = 2ax + b = 0 para y = ax2 + bx + c
Usando esta relación vértice = -2 x + 30 = 0 o x = 15.
Agregar 15 plantas producirá (20 + 15) x (50 – 15) = 1225 tomates.
En el vértice, los valores pueden ser mínimos o máximos. Obviamente, este no es un valor mínimo porque el rendimiento de 1225 tomates es mayor que el rendimiento actual de 1000 tomates.
Problema de Tom: Esto es algo que sucedió en la tienda de mi papá. Entró una señora con un retrato con una relación de alto a ancho de 4/3. Quería ampliar la imagen a 192 pulgadas cuadradas y quería saber cuál sería la altura y el ancho de la imagen ampliada. Mi papá es muy inteligente y me dijo que lo descubrió usando una ecuación cuadrática.
Digamos que el ancho es x pulgadas. Entonces la altura será 4x/3 y el área será 4x2/3. Por lo tanto,
4x2/3 = 192 o x2 = 144 o x = ±12 pulgadas de las cuales solo x = 12 pulgadas tiene sentido.
Entonces, el ancho de la imagen sería de 12 pulgadas y su altura sería de 12 por 4/3 o 16 pulgadas. Verificando el área, 16 pulgadas x 12 pulgadas = 192 pulgadas cuadradas.
Problema de Jorge: Juego baloncesto pero no soy muy alto. Necesito saltar para clavar la pelota de modo que mis pies estén a 2.5 pies del suelo. El entrenador me dijo que su profesor de kinesiología le enseñó la ecuación para saltar a la altura de 16t2 -12t donde t es el tiempo en segundos que estoy en el aire. ¿Cuánto tiempo tendré que estar en el aire para poder encestar?
Esto es similar al problema de la animadora Kim excepto por las unidades. Todo se da aquí en pies. La relación será 16t2 -12t = 2,5 o 16t2 -12t – 2,5 =0.
Para una ecuación cuadrática ax2+ bx + c = 0, x = (-b ± (√(b2 -4ac))/2a
Por lo tanto t = ((12 ± √ ( 122 – 4 x 16 x (-2.5)))/2 x 16 = 0.92 o menos 0.17 seg. Estar en el aire por tiempo negativo no tiene sentido. Entonces Jorge tendrá que saltar estar en el aire durante 0,92 segundos para poder hacer un mate.
Parte superior de la página e índice del sitio