
La vieja amiga Olivia visitó a Sara
Nana le dijo a Sara que Olivia llamó y quería venir a visitarla el sábado. Olivia estaba con Sara en los grados sexto a octavo, pero luego los padres de Olivia se mudaron a otro distrito de la ciudad y las dos amigas terminaron yendo a escuelas diferentes. A pesar de que eran buenos amigos, de alguna manera no se conectaron después de eso a pesar de que Olivia tenía toda la información de contacto de Sara. Habían pasado casi dos años desde la última vez que se habían visto. Nana también tenía buenos recuerdos de esta chica.
Sara: Gracias Nana. ¿Es esta la Olivia Sánchez de mi octavo grado?
Nana: Sí, y le dije que podía venir el sábado por la mañana. Tendría samosas listas para ella. Ella solía amarlos.
Sara: Sí, los amaba. ¿Sabes que les decía empanadas indias? Me aseguraré de quedarme en casa el sábado para estar con Olivia todo el día si ella lo desea.
Olivia se acercó como se esperaba. Había crecido un poco como se esperaba, pero nada fuera de lo normal. Todavía tenía una figura pequeña, rebotaba mucho y estaba tan alegre como siempre. Los dos amigos estaban tan contentos de verse. Recordaron como si estuvieran juntos incluso ayer. Tenían tantos recuerdos para compartir sobre cada niño y niña en esa escuela secundaria y también tenían preguntas sobre dónde estaban todos ahora, qué hacían y con quién salían. Por supuesto, como niñas adolescentes, a ambas les interesaba hablar sobre niños. Olivia tenía algunos chicos como amigos, pero ninguno que ella pensara que era material para un novio. Estaba encantada de saber que Sara había encontrado a Johnny.
Olivia: Entonces, ¿cómo os conocisteis tú y Johnny?
Sara: Vive cerca de mi camino a la escuela y anda en bicicleta a la escuela todos los días. Me vio un par de veces de camino a la escuela, se bajó de la bicicleta y comenzó a caminar conmigo. Luego nos volvimos a encontrar en la cafetería. Una cosa llevó a la otra y ahora caminamos juntos a la escuela todo el tiempo. Supongo que le gustó lo que vio.
Olivia: ¿Es lindo?
Sara: Escucha, no he visto tu nueva escuela. ¿Que tan lejos está?
Olivia: A poco menos de tres kilómetros de aquí pero no respondiste mi pregunta sobre Johnny.
Sara: No respondí porque era una pregunta tonta. Le dirá qué. Quiero ver tu nueva escuela. Caminaremos de ida y vuelta. Le preguntaré a Johnny si quiere venir. Así podrás conocerlo y darme la respuesta a tu propia pregunta.
Sara llamó a Johnny. Estaba más que feliz de venir a dar un paseo con ellos. Caminaron juntos a la escuela de Olivia. Por supuesto, Johnny vino con su nueva bicicleta que tenía todos los artilugios. Como la escuela estaba a unos tres kilómetros de distancia, la caminata les dio a las dos niñas un poco más de tiempo para cotillear y conocerse.
La escuela de Olivia era triangular.
Cuando llegaron a la escuela de Olivia, Sara y Johnny quedaron asombrados por la forma del edificio. La escuela secundaria de Sara y Johnny tenía un edificio circular pero este tenía una base triangular. El frente de la escuela corría de este a oeste. La pared del lado izquierdo estaba en ángulo, y el lado derecho era tan estrecho que casi no tenía pared.
Sara: ¿Qué tan grande es esta escuela, cuál es su área?
Olivia: no lo se Nunca pensé en eso.
Johnny estaba muy emocionado. Tenía un nuevo proyecto para su bicicleta: encontrar el área de la escuela y se lo contó a Sara y Olivia.
Olivia: No puedes medir la longitud de la pared trasera de la escuela. Hay una valla que te impide llegar a la parte de atrás. Al otro lado de la valla, hay una gran empresa con candados de alta seguridad en la puerta de su complejo.
Sara sonrió como si supiera algo.
Sara sonrió como si supiera algo y le dijo a Olivia que no se preocupara. Johnny usó su bicicleta para medir la longitud de la pared frontal de 100 metros. También encontró que el ángulo entre las paredes frontal y lateral era de 105°, y que la longitud de la pared lateral era de 70 metros. Pensó que eso era todo lo que podía medir debido a las diferentes restricciones, pero Sara le dijo que eso era suficiente. No podían entrar a la escuela porque estaba cerrada por ser sábado. Así que decidieron dar un paseo de regreso a la casa de Sara. Sara y Olivia continuaron con su charla. Después de todo, tenían mucho para ponerse al día después de los dos años. Johnny no estaba realmente interesado en esa conversación, pero tenía su bicicleta para mantenerlo comprometido y feliz.
Los tres regresaron a la casa de Sara. Por supuesto, Nana les tenía preparadas las samosas. Estaban saboreando los bocadillos cuando Olivia interrumpió y preguntó cómo iban a encontrar el área de su escuela.
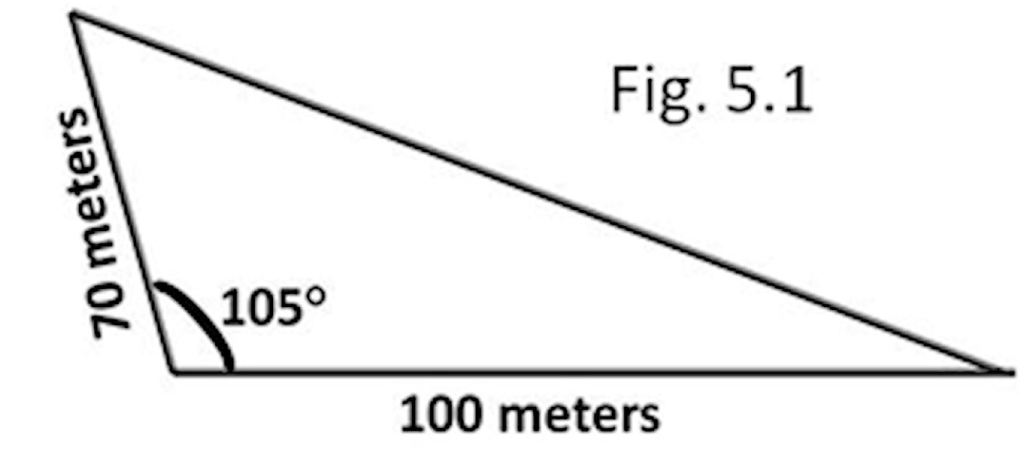
Johnny hizo este dibujo (Fig. 5.1) y dijo: La base de la escuela es un triángulo con una pared frontal de 100 metros, una pared lateral de 70 metros y un ángulo de 105° entre las dos paredes. Sara, ¿qué hacemos ahora? Dijiste que era suficiente información.
Sara modificó la foto de Johnny.
Sara: Modifiquemos un poco tu imagen. Primero, vamos a etiquetarlo. AB es la pared frontal de la escuela, AC es la pared lateral y BC es la pared trasera. El ángulo BAC es de 105°. Voy a dibujar una línea hipotética para extender el frente hasta D, y dibujaré una línea vertical desde C para cruzarla en D tal que el ángulo ADC sea de 90° (Fig. 5.2).

Johnny interrumpió tan pronto como Sara dibujó estas líneas punteadas: Ahora, esto es muy simple. A partir de esta imagen, podemos encontrar tanto la longitud de la pared trasera como el área de la escuela.
olivia: eso creo Ángulo DAC= 75° porque es complementario al ángulo BAC que es de 105°. Usando las longitudes de los lados:
CD/CA = sin 75° y DA/CA = cos 75°. ¿Cuáles son los valores de sin y cos para 75°?
Johnny: sin 75° = 0,9659 y cos 75° = 0,2588. Eso significa CD = 0,9534 x CA = 0,9659 x 70 o 67,61 metros y DA = 0,2588 x CA = 0,2588 x 70 = 18,12 metros.
Olivia: Eso está bien. Tenemos dos triángulos en ángulo recto: uno es DAC hecho en el lado izquierdo de la escuela. Tiene una altura de 67,61 metros y una base de 18,12 metros. El segundo es el triángulo más grande DBC con la misma altura pero una longitud de 100 + 18,12 = 118,12 metros.
Dimensiones de la escuela
Sara: Recuerda que el área de cualquier triángulo es altura x base/2.
Johnny: Sí, lo recuerdo de mi clase de geometría. Entonces, el área del edificio de la escuela es 67,61 x 100/2 (alto x pared frontal/2), que es 3380,7 metros cuadrados. Así que eso está hecho. Olivia, te dije que Sara nos ayudará a resolver esto. Ahora, ¿qué pasa con la pared trasera?
Olivia: Eso es fácil. Recuerda el teorema de Pitágoras de la geometría.
Johnny: Lo recuerdo y también Sara me lo recordó hace dos semanas. Está:
Hipotenusa2 = base2 + altura2. Para el triángulo DBC, sería
BC2 = DB2 + DC2 o BC2 = 118,122 + 66,74 2 o BC = 136,1 metros.
Así que la pared trasera tiene 135,67 metros de largo.
Olivia: Estoy tan feliz y tengo ganas de saltar de alegría. Voy a hablar con la oficina del director y publicaré las longitudes de las paredes en el tablón de anuncios de la escuela. Espero que no te importe. Les daré todo el crédito por ello.
Johnny: No menciones nuestros nombres, por favor. ¿Por qué los estudiantes externos vendrían a su escuela para este tipo de mediciones? Además, todo lo que hice fue divertirme un poco con mi bicicleta. De todos modos, tengo que irme a casa porque mi mamá debe estar esperándome,
Sara: Olivia, ustedes hicieron todos los cálculos, solo ustedes podrían haberlos hecho si no estuviéramos aquí. Solo dibujé las líneas punteadas. Jhonny tiene razón. No menciones nuestros nombres. Sin embargo, hay una cosa más que debes hacer antes de hablar con los chicos de tu escuela.
Olivia: que es eso?
Sara: ¿Cuál será tu respuesta si el profesor de Matemáticas te pregunta por qué diste solo un ángulo y no los tres?
Olivia: Porque medimos solo uno.
Determinación de todos los ángulos
Sara le mostró a Olivia el libro Trigonometría para mostrar cómo podía obtener todos los ángulos de este triángulo. Olivia lo leyó con los ojos muy abiertos como si no creyera que pudiera captar los otros dos ángulos. Ella leyó la regla llamada la ley de los sines: sin A/a = sin B/b = sin C/c y dibujó este dibujo. En esta imagen, el ángulo A era de 105° como lo había medido Johnny y el lado a = 136,1 metros.
Como sin A = sin 105° = 0,9659, el valor de sin A/a = 0,007097. Entonces los valores de sin B/b y sin B/b también deben ser 0.007097. con c =70 metros, sin B = 0,007097 x 70 = 0,4968 o ángulo B = 29,8°. Sin C/c = 0.007097 = 0.7097 porque c = 100 metros o ángulo C = 45.2°. Como 105 + 29,8+ 45,2 = 180, que debería ser la suma de todos los ángulos de un triángulo, la respuesta se comprobó.

Olivia: Gracias Sara. Ahora publicaré una nota en el tablón de anuncios con las longitudes de los tres lados y los ángulos para la escuela.
Sara: Así que todo está bien. No me dijiste lo que piensas de Johnny.
Olivia: No me pongas celosa. Es lindo, inteligente y te ama. Ojalá tuviera un novio como él.
Olivia vio al director de la escuela y le pidió permiso para poner una nota sobre lo que había averiguado sobre la escuela. El director le pidió que verificara la información con su maestro de Matemáticas. Lo hizo y luego escribió una nota sobre estos datos interesantes sobre la escuela: forma triangular obtusa, longitudes de las paredes, los ángulos entre ellas y el área del edificio de la escuela. Olivia recibió un buen elogio de sus compañeros de escuela. Algunos de ellos tenían curiosidad sobre los detalles de cómo ella determinó todo esto. Ella les contó todo. Por supuesto, solo sus amigos cercanos obtuvieron los detalles sobre su visita a Sara y los detalles sobre el lindo novio de Sara.
Desafío
Como a Johnny le había ido tan bien en la escuela el semestre anterior, sus padres le compraron un dron con control remoto. Quería volarlo y le pidió a Sara que lo acompañara al parque. Por supuesto, Sara estuvo de acuerdo porque le encantaba estar con él. También trajo el sextante de su papá. Johnny estaba pilotando el dron y lo tenía en un lugar inmóvil y le dijo a Sara, que estaba sentada a su lado: “Me pregunto qué tan lejos está el dron”. Sara midió que el dron estaba en un ángulo de 45° desde el suelo desde donde ella estaba. Caminó unos 20 metros hacia el dron y ahora el ángulo desde el suelo era de 60°. Habría tenido que caminar aún más para estar debajo del dron. A partir de esto, Sara le dijo a Johnny qué tan lejos estaba el dron de él. ¿Puedes averiguar qué hizo esta chica prodigio?

Solución: Dibujemos un triángulo desde la primera posición de Sara en A, la segunda posición a 20 metros de distancia en B y el Drone en C (Fig. 10.5). Prolonga la línea AB hacia D.
Dado: Distancia AB = 20 metros, ángulo CAB = 45°, ángulo CBD = 60° (nota que Sara tendría que caminar más hacia el punto D para estar debajo del dron.
Ahora, en el triángulo ABC, el ángulo A = 45°, el ángulo B = 180° – 60° = 120° (ángulo complementario), y el ángulo C = 180°- 45°-120° = 15° (suma de todos los ángulos de un triangulo mide 180°).
Según la identidad trigonométrica llamada ley de los senos:
sin A/a = sin B/b = sin C/c.
Lado opuesto al ángulo B = b (AC), y opuesto al ángulo C = c (AB = 20 metros).
De la ley de los senos, sin B/b = sin C/c o sin 120°/b = sin 15°/20 o 0.866/b = 0.259/20 o
b/0.866 = 20/0.259 o b = 0.866 x20/.259 = 66.9 metros.
El dron de Johnny está aproximadamente a 66,9 metros de él.