
Patios escolares: salón de actos, clase de ciencias, clase de trigonometría y cafetería
Consigue un helado y camina hasta la escuela.
Era otro agradable día de verano con temperaturas moderadamente altas que se hacían cómodas con la brisa ocasional, el tipo de día en el que a la mayoría de los adolescentes les gusta salir a las heladerías y pasar el rato. Johnny telefoneó a Sara y le preguntó si podían ir a comprar un helado. Fueron juntos y consiguieron el helado. Por supuesto, Johnny se llevó su nueva bicicleta de la que estaba tan orgulloso. Después de esto, decidieron no quedarse por allí sino dar otro paseo por su escuela. Uno podría suponer que a Johnny le había gustado su última visita a la escuela. A partir de esa experiencia, Johnny estaba seguro de que su novia no iba a desperdiciar esta oportunidad de empujarlo más hacia ser un genio Trig. ¿Qué más podría pedir? Estar con su amante sexy y su hermosa bicicleta nueva. Sara lo amaba y siempre quiso estar con él. Dieron el mismo paseo por el camino circular alrededor de su escuela que la vez anterior.
Sara: johnny ¿Sabes que puedes obtener tablas de valores para funciones trigonométricas para diferentes ángulos? También puede obtener estos valores utilizando la mayoría de las calculadoras. Así que traje mi calculadora conmigo. Comprobaremos la precisión de tu bicicleta en las distancias Norte-Sur y Este-Oeste.
Johnny: No dudes de mi hermosa bicicleta. Tiene un aspecto sexy. ¿No crees?
Sara dijo de manera juguetona: ¿Más sexy que yo? No te atrevas a decir que sí, simplemente cállate. Comencemos en el mismo lugar que la última vez. Recuerde, comenzamos en el camino circular alrededor de la escuela en la puerta noreste de la escuela. En cualquier momento, cuando me diga nuestro ángulo de rotación en grados desde su bicicleta, le diré las distancias esperadas y puede igualarlas en su bicicleta.
Comenzaron a caminar y luego Johnny se detuvo.
Mi bicicleta dice una rotación de 30° desde el inicio original
Johnny: Mi bicicleta dice una rotación de 30° desde el inicio original.
Sara: Mi calculadora dice que sen 30° es 0,5 y cos 30° es 0,866. Como la hipotenusa mide 100 metros, recorrimos 50 (100 por 0,5) metros al norte y 13,4 metros al oeste (100 – 100 cos 30° o 100 – 86,6 metros).
Johnny: Sí. Eso es lo que dice mi bicicleta. Así que la cosa de pecado y cos funcionó.
Johnny siguió adelante pero luego se detuvo y dijo 90°. Preguntó los valores de sen y cos.
Los valores son obvios para sen 90° o cos 90°
Sara se rió a carcajadas. Cuando Johnny le preguntó qué tenía de divertido 90°, ella dijo: No necesito mi calculadora para eso. Hemos ido tan al norte como pudimos donde la altura es la misma que la hipotenusa del triángulo y eso significa que su razón es 1, que es sen 90°. También hemos viajado 100 metros al Oeste. Estamos exactamente al norte del centro de la escuela, lo que significa que cos 90° es 0.
Johnny tenía la imagen de la escuela y este camino en su mente y recordó dónde le mostraría el mapa en la parte más al norte del camino. Entendió la situación hasta cierto punto, y siguió adelante. Empezaron a pasar cosas graciosas. Su distancia hacia el norte comenzó a disminuir, pero la distancia hacia el oeste aún aumentó. Se lo mostró a Sara quien le explicó con esta imagen (Fig. 2.1)
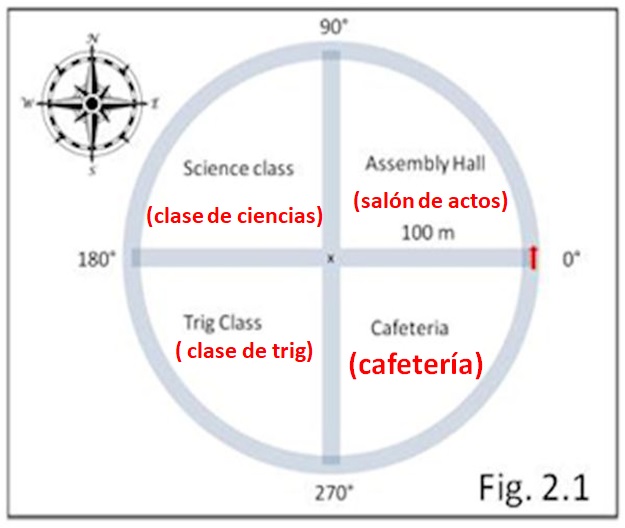
¿Qué sucede alrededor de los 90°?
Sara: Recuerda en Álgebra, el origen es donde el eje X y el eje Y se cruzan entre sí. La línea Este-Oeste será entonces el eje horizontal o el eje X y la línea Norte-Sur será el eje vertical o el eje Y. La altura alcanza el máximo en la parte superior del eje Y, que es un ángulo de 90°, y luego comienza a disminuir. La disminución significa que ya no vas al norte sino que has comenzado a moverte al sur. Sin embargo, continúas moviéndote hacia el oeste.
Johnny: Ahora, la bicicleta da una rotación total de 150°.
Sara: Recuerda, un ángulo de 150° te dará la misma altura que un ángulo de 30° pero en el segundo cuadrante. Aquí los valores de la altura son positivos pero los de la base son negativos porque te has ido al lado izquierdo del origen.
Johnny: Esto es confuso. ¿Significa eso que sen 150° sería lo mismo que sen 30°?
Sara: Sí, pero cos 150° no será lo mismo que cos 30°.
Johnny: Lo entiendo, será lo mismo pero negativo. cos 30° = 0,866. Entonces, cos 150° = – cos 30° = – 0.866. Mira, no soy un tonto. ¿El valor de tan también cambia de signo?
Cine después de la escuela
Sara: Si genio. Ahora, dime, si divides la escuela en cuatro cuadrantes, ¿dónde está el Salón de Actos y quién va allí?
Johnny: Sería en el primer cuadrante. Todos nosotros vamos allí para la asamblea, los estudiantes y los profesores.
Sara: Tu clase de Ciencias está en el segundo cuadrante y la clase de Trigonometría está en el tercero.
Johnny: La cafetería está en el cuarto cuadrante. Ese es mi lugar favorito. Recuerda, ahí es donde nos conocimos hace dos años.
Sara: Todos van a la Asamblea (primer cuadrante) positivamente – sin, cos y tan. Solo el pecado es positivo en el cuadrante de Ciencias (segundo), solo el bronceado es positivo en el cuadrante Trigonométrico (tercero) y el coseno en el cuadrante de Cafetería (cuarto).
Johnny: Esa es una buena manera de recordar.
Sara: Supongo que la escuela de mi papá no era redonda como la nuestra. Dijo que su maestra les dijo que recordaran “cine después de la escuela” para todos, pecado, bronceado y cos. Si no te gusta ir al cine, también puedes decir “Chocolates después de la escuela” o “Todas las tazas de té plateadas”. Hay una cosa mas. La mayoría de los profesionales no hablan de los ángulos en grados. Usan radianes. La idea es que dar la vuelta a un círculo completo es 2π radianes en lugar de 360°. Recuerda, aprendimos en geometría que π es la relación entre la circunferencia de un círculo y su diámetro. Tiene un valor aproximado de 22/7. Entonces, un radián es 2π/360 o alrededor de 57°. En ese sistema, el primer cuadrante es de 0 a π/2, el segundo de π/2 a π, el tercero de π a 3π/2 y el cuarto de 3π/2 a 2π.
Gráficas de funciones trigonométricas
Supongo que esta fue una lección complicada. Aun así, Sara le mostró las gráficas de los valores de sen x, cos x y tan x para diferentes valores de x (figura 2.2).

Johnny notó que los valores de sen x y cos x en las gráficas oscilaban solo entre 0 y 1. Eso tenía sentido porque la altura o la base de un triángulo rectángulo no puede exceder la longitud de la hipotenusa. Además, fue interesante que sen x fuera positivo solo en los dos primeros cuadrantes y cos x en el primero y cuarto. También notó que cos x decrecía con el aumento de sen x. Eso también tenía sentido porque sen2x + cos2x =1 o sen2x = 1 – cos2x.
El más intrigante fue el gráfico de tan x. No se detuvo en 1 como lo hicieron los gráficos sen x y y cos x, sino que siguió aumentando en su valor. Además, fue positivo justo antes de los 90°, y de repente tomó un valor negativo muy grande. Lo mismo sucedió alrededor de los 270°. Le recordó a un chico que estaría extremadamente feliz en un momento y luego, de repente, comenzaría a llorar.
A Johnny le resultó fácil entender al profesor de Trigonometría y hacer la tarea. Johnny y Sara habían hecho todas las tareas asignadas correctamente. Ambos también obtuvieron el 100% en el examen de mitad de período de Trig. Johnny saltaba de alegría e invitó a cenar a Sara.
Desafío
Desafío: Johnny y Sara estaban hablando y viendo la televisión cuando vieron una imagen de la rueda de la fortuna High Roller en Las Vegas. La rueda tiene un diámetro de 520 pies (158,5 metros) y 28 cajas de asientos separadas por igual. Da una vuelta cada 30 minutos. Maravillados por el sitio, imaginaron dónde se sentarían si fueran juntos. Debido a que es costoso, irían solo por una rotación. Decidieron que Sara se sentaría primero y luego, después de que la rueda hubiera girado un poco, Johnny se sentaría a 7 cajas de distancia. Cuando llegaban a la misma altura, se saludaban. Sería divertido. ¿A qué altura sucedería eso? Sara lo sabe, mira si tú lo sabes.

Solución: Hay 28 cajas en la rotación completa (360°) de la rueda (Fig.10.3). Sara (S) ya ha viajado a 7 cajas de distancia (360° x 7/28 = 90°) cuando Johnny (J) se sienta en su caja. El radio de la rueda es la mitad del diámetro o 158,5/2 = 79,25 metros. Dibuja una línea vertical desde C el centro de la rueda. S y J estarán a la misma altura solo cuando el ángulo SCV = ángulo VCJ pero sabemos que el ángulo SCV + el ángulo VCJ = 90° y, por lo tanto, el ángulo VCJ = 45°. Dibujar una perpendicular desde CJ sobre la línea CV da el triángulo rectángulo CVJ con el ángulo VCJ de 45°. Por lo tanto CV = 79,25 cos 45° = 79,25 x 1/√2 = 56,04 metros. Entonces la altura total será la altura al centro más 56,04 metros = 79,25 + 56,04 metros = 135,3 metros.
Tenga en cuenta que también podrían volver a alcanzar la misma altura si hubieran pagado por más de una rotación. Averigua esto por ti mismo.