
Nuevas formas de llamar la atención de los estudiantes
La Sra. Rania Ali enseñó en una escuela primaria ubicada en un barrio pobre. La mayoría de los estudiantes venían allí porque tenían que hacerlo. Sus padres recibían una cierta cantidad de apoyo vital del gobierno si sus hijos asistían a la escuela. Así que los padres les dijeron a los niños que tenían que estar en la escuela. Los niños tenían, en el mejor de los casos, un interés marginal en el aprendizaje. La Sra. Rania Ali estaba consciente de su desafío, pero la gran maestra encontró nuevas formas de llamar la atención de sus alumnos. Esta es la historia del día en que tuvo que enseñar sobre ángulos como una de las lecciones de geometría.
La Sra. Ali le pidió a uno de los niños que viniera y se enfrentara a la clase. Luego le pidió al niño que girara a la izquierda, a la izquierda una y otra vez hasta que estuvo frente a la clase. Luego le dijo a la clase que el niño había girado un círculo completo. La rotación se midió como un ángulo, y para un círculo completo el ángulo fue de 360°.

Balancín y ángulos
Algunos estudiantes se divirtieron, pero la Sra. Ali tuvo que hacer más para que se interesaran. Así que les mostró la imagen de un balancín. El balancín era una tabla plana con lados que podían subir o bajar. La medición del ángulo mostraría que la parte superior formaba un ángulo de 180°. La otra mitad del ángulo se formó debajo del tablero y también era de 180° (no se muestra aquí). Así, los ángulos por debajo y por encima del tablero se suman a una rotación completa de 360°.
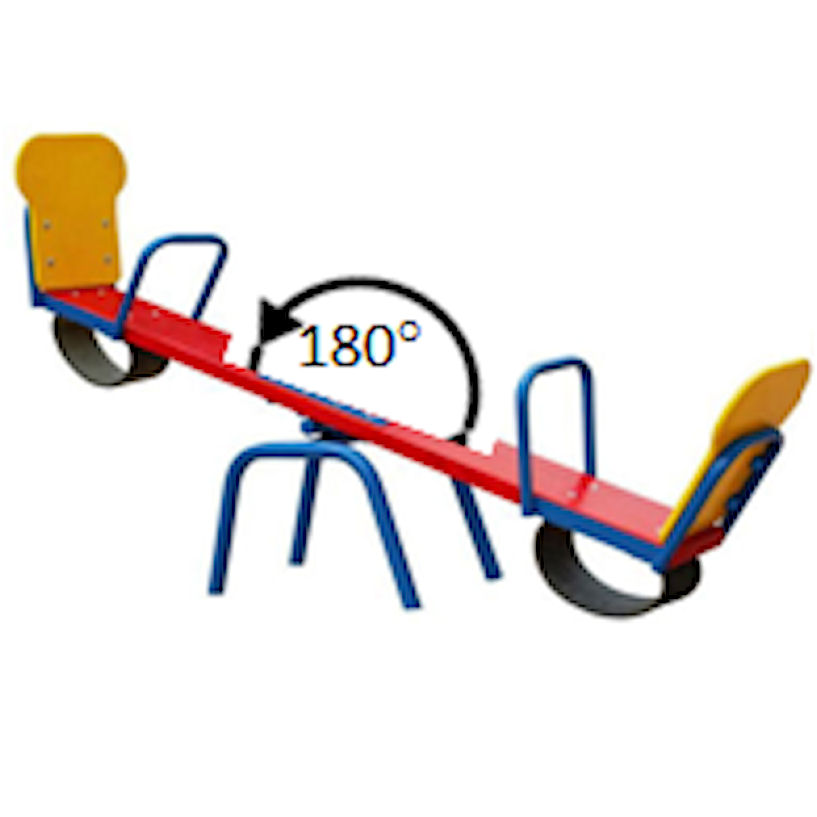
A los niños les encantó hasta ahora, pero se preguntaban qué iba a mostrar la Sra. Ali a continuación.
Sra. Ali: Viste que el ángulo en la superficie plana del tablero era de 180°. Incluso si cortaras este ángulo en dos o tres partes, su suma sería 180°. Así que recuerda que la suma de todos los ángulos formados en una línea recta es 180°.
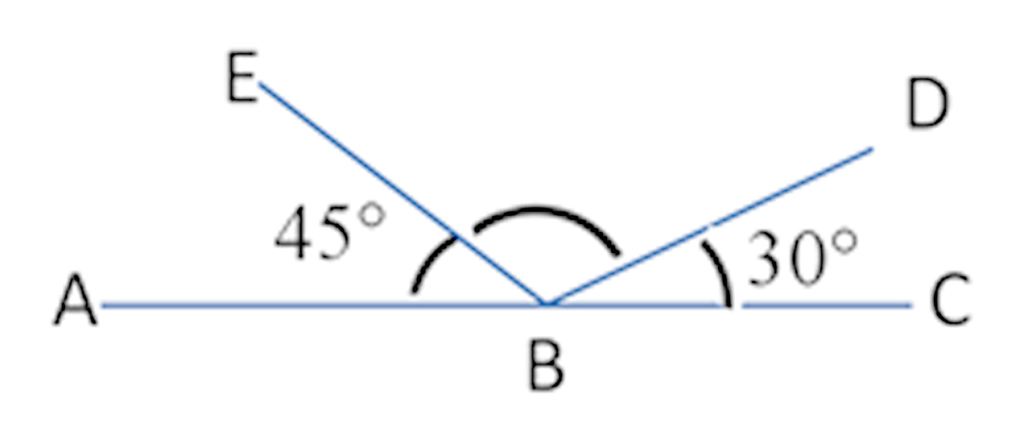
Aquí hay un ejemplo. Sobre la recta ABC se forman los ángulos ABE, EBD y DBC. El ángulo EBD será 180° – 45° -30° = 105°.
¿Recuerdas una rueda de la fortuna?
Ahora, ¿recuerdas cómo es una rueda de la fortuna? Les voy a mostrar una rueda de la fortuna con 8 gandolas para que se sienten los niños. El centro de la rueda está marcado con la letra C. Está conectado con radios a las gandolas. Alia, Arisha, Mehak, Fateh y Rehan están sentados en las gandolas como se muestra. Primero, dime cuál es el ángulo entre el radio de la barra gandola de Alia, el centro y el radio de la barra gandola de Arisha. Supongo que Alia y Arisha tienen que resolver esto.

Alia: Sra. Ali, hay 8 radios en la rueda de la fortuna. Eso significa que el ángulo entre dos radios uno al lado del otro es 360 dividido por 8, que es 45°.
Entonces el Alia-Center-Arisha será de 45°.
Sra. Ali: ¿Todos entendieron eso? Ahora Mehak tiene que decirme el ángulo Alia-Centro-Mehak.
Mehak: Este ángulo es tres octavos de un círculo completo. Entonces será 360 x 3/8 o 135°.
Sra. Ali: Rehan, dime el ángulo entre tú y Alia.
Rehan: Sra., puedo ir a la parte inferior de la rueda a Alia. Eso será tres octavos de todo el círculo. Entonces será 135°. Sin embargo, si Alia llegara desde la parte superior de la rueda, el ángulo sería de 360 menos 135, que es 225°.
¿Qué hay de mí?
Rajab: ¿Cómo es que solo cinco de ellos pueden viajar en la rueda de la fortuna? ¿Qué hay de mí?
Sra. Ali: Todos podrán montar. Una gran rueda de la fortuna viene a continuación. Aquí está. Rajab, ¿cuántas gandolas tiene?
Rajab: Conté 36 góndolas. Todos los de nuestra clase pueden continuar con espacio para los demás.
Sra. Ali: Si estuviera sentada en una gandola e Imtiaz estuviera en la siguiente, ¿cuál sería el ángulo entre su radio, el centro y el siguiente radio?
Rajab: El círculo completo es de 360° y esto sería 1/36 parte o 10°.

Sra. Ali: Buen trabajo, Rajab. Espero que todos se hayan divertido con las ruedas de la fortuna. Ve a casa y busca más de ellos en Internet. Mira cuántos diferentes puedes encontrar. Encuentra los ángulos entre un radio y el que está al lado. También puede mirar las ruedas de los automóviles y las llantas, ya que también pueden formar ángulos. No hay tarea, hoy. Solo diviértete con las ruedas.
Desafío
¿Cuál es el ángulo más pequeño entre las manecillas de hora (corta) y minutero (larga) en las diferentes horas que se muestran en los relojes a continuación?
Solución: Un círculo completo son 360°. En el reloj, los números del 1 al 12 dividen este círculo en 12 partes iguales, cada una de las cuales es 360/12 o 30°. A la 1 en punto, la manecilla larga está en el 12 y la manecilla corta apunta al 1, a solo un número de distancia. Por lo tanto, el ángulo entre las dos manos es de 30°. A las 3 el ángulo entre las dos manos será de 3 x 30 o 90° ya las 4 será de 4 x 30 o 120°. A las 8 en punto se podría decir que las manecillas están separadas por 8 números si cuentas 1,2…8 pero solo 4 números si cuentas 8,9,10 y 11. Entonces el ángulo entre ellos podría ser de 240° o 120° pero se nos pide el ángulo más pequeño. Eso será 120°. De manera similar, en 10, el ángulo más pequeño será de 60°.
