Priya la buscavida
Priya siempre había sido una emprendedora. Ahora, a la edad de 16 años, trabajaba con su mamá Jenna en su tienda que imprimía y vendía camisetas con diseños impresos. Hicieron camisetas para todos los que vinieron allí y también recibieron pedidos especiales de los equipos. Priya ganaba un poco más que el salario mínimo y trabajaba solo medio tiempo en la tienda porque todavía estaba en la escuela secundaria.
Priya estaba tomando un curso de Geografía. El examen final valía el 40% de la nota de la asignatura. El maestro ofreció a todos en la clase la opción de hacer un proyecto de Geografía en lugar del examen final. Priya obtuvo calificaciones muy bajas en este examen. Pensó que sería mejor hacer el proyecto en el que podría trabajar a su propio ritmo.
El ingenioso proyecto de geografía de Priya
Priya era una chica muy inteligente. Le propuso a la maestra que haría un proyecto sobre: ”de donde vienen los clientes a la tienda de camisetas de su mamá”. Pensó que podría hacer este proyecto en el trabajo en el tiempo de Jenna. Con la esperanza de que pudiera ayudar a mejorar el negocio, su madre accedió. El profesor de Geografía aprobó el proyecto considerando que se acercaba lo suficiente a ser un trabajo de Geografía, y también porque la idea era práctica.
Los clientes daban sus direcciones y números de teléfono cada vez que pedían camisetas en la tienda. Vendrían y recogerían sus pedidos en o después de la fecha de vencimiento. Priya sacó los registros de la tienda de los últimos dos meses. Para cada cliente, buscó la dirección y encontró la distancia entre esa dirección y la tienda usando el “mapa de Google” en su computadora portátil. Ella registró estas distancias como sus datos. Dividió los datos de la siguiente manera: clientes que venían de menos de 1 kilómetro de distancia, entre 1-2 kilómetros de distancia y más de 2 kilómetros de distancia. Concluyó que muy pocos clientes venían de más de 2 kilómetros. Ella escribió su informe de proyecto con esta conclusión.
El maestro dijo: “Puedes hacerlo mejor, mucho mejor”
Le pidió a su profesor de Geografía que viera el informe y diera su opinión sin marcarlo. El maestro miró el informe y dijo: “Puedes hacerlo mejor, mucho mejor”. La maestra también dijo que debido a que este era un proyecto independiente, no debería pedirle ayuda.
La pobre Priya estaba sentada en la cafetería de la escuela con la cabeza gacha. Ella estaba perpleja. Ella no sabía qué hacer. Vino su amiga Kate, pero Priya no estaba de humor para charlar. Kate era una buena amiga y no se dio por vencida con ella, y se sentó de todos modos. Kate le preguntó a Priya por qué estaba de tan mal humor.
Priya: Es mi proyecto de Geografía. El profesor no está contento con eso. Podría reprobar Geografía.
Kate: Déjame ver el informe.
Priya le dio el informe a Kate, quien echó un vistazo rápido pero no sabía cómo se podía mejorar el informe. Priya pensó que estaba condenada. De repente, Kate comenzó a hablar.
Kate le presentó a Priya a Sara
Kate: Ahí está Sara. ¿Por qué no hablas con ella? Puede ser que ella te pueda ayudar. Ella es un verdadero genio.
Priya: Por un lado, no sé si tomó Geografía o no. Segundo, ¿por qué me ayudaría incluso si pudiera? Ella es dos años mayor que nosotros y ni siquiera me conoce.
Ser una buena amiga Kate no renunció. En cambio, ella fue bastante insistente y dijo: Ella es muy inteligente. Le encantan los desafíos. Además, qué tienes que perder hablando con ella. Ser amable con ella. Hablé con ella una vez. Os presentaré a los dos.
Kate fue donde estaba sentada Sara, la saludó y se sentó. Priya siguió a Kate.
Kate: Hola Sara. soy Kate Nos conocimos una vez, pero no sé si me recuerdas. Esta es mi amiga Priya.
Sara; Hola Kate, me acuerdo de ti. Encantado de conocerte Priya.
Priya: He oído muchas cosas buenas sobre ti. Todos en la escuela saben cómo ayudaste a Johnny con Trigonometría.
Sara: Sí, lo hice. El es mi novio. ¿Es eso un problema?
Priya: Tengo un problema, pero no es que seas inteligente y hayas ayudado a tu novio. Te admiro por eso. Ojalá tuviera a alguien inteligente como amigo que pudiera ayudarme.
Sara: Dijiste que tenías un problema.
Kate: Creo que tiene un desafío para ti.
Priya: Mira, tengo un problema y acudí a ti porque eres inteligente. Entenderé si crees que no debería haber venido. Debes tener mucho trabajo que hacer.
Sara: Primero, déjame escuchar tu problema y luego decidiré si puedo ayudarte o no.
Priya le contó a Sara sobre su proyecto de Geografía y le mostró el informe. Sara lo revisó rápidamente.
Sara: Sé cómo se podría mejorar este proyecto.
Dijiste que esto es para un curso de Geografía. Luego ponle algo de Geografía. Dijiste que tenías las direcciones de los clientes. Tome un mapa del área. Marque su tienda en él. Luego marque cada cliente en el mapa con un punto.
Priya: Gracias, podría hacerlo fácilmente.
Sara: ¿Dónde está tu tienda?
Priya le dio la dirección exacta.
Sara sonrió y dijo: ¿Quieres una A+ en el proyecto?
Priya: Sí, ¿cómo?
Sara: Primero trae el mapa con todos los puntos y luego te cuento.
Priya: Gracias Sara. Lo haré.
Priya estaba en la nube 9 con la mención de obtener una A+ y agradeció a su mejor amiga Kate por presentarle a Sara. Trabajó duro durante tres días y puso un punto para la dirección de cada cliente en el mapa del área y un cuadrado para la ubicación de la tienda. Luego le llevó el mapa marcado a Sara (Fig.8.1).

Sara: ¿No se parece más a un proyecto de Geografía ahora? Tienes un mapa con un río y todo. ¿Tu mamá está contenta con eso?
Priya: Mi mamá dijo que este mapa le dijo mucho más que el último informe. Apenas tenemos clientes del otro lado del río.
Sara: El río fue la razón por la que sonreí la última vez que me dijiste la dirección de tu tienda. Si escribes un informe basado en este mapa, tu profesor debería darte fácilmente una B+ o incluso una A-, pero para obtener una A+ tendrás que aprender algo nuevo. Lo he estado pensando desde que hablamos la última vez.
Priya: ¿Qué tengo que aprender?
Sara: Puedo trabajar contigo pero tienes que prestar atención incluso cuando se pone difícil.
Priya: Estoy totalmente de acuerdo. Dale.
Sara encendió su computadora portátil y trajo una imagen de un tablero de dardos.
Priya: ¿Tengo que aprender a jugar a los dardos? Eso ya lo se.
Sara: No, vamos a usar el tablero de dardos solo para aprender algo.
Priya: Bien, ¿empezamos con la diana? Eso es difícil de acertar con un dardo.
Sara: ¿Recuerdas que en Matemáticas aprendiste sobre el eje X y el eje Y? El origen era el punto donde se cruzaban los dos ejes.
Priya: Sí, lo recuerdo. ¿Vamos a llamar a la diana el origen?
Sara: Sí, diremos que la diana interior es el origen. Hay muchos círculos a su alrededor. ¿Qué círculo está más cerca del origen?
Priya: La diana exterior es el círculo más cercano.
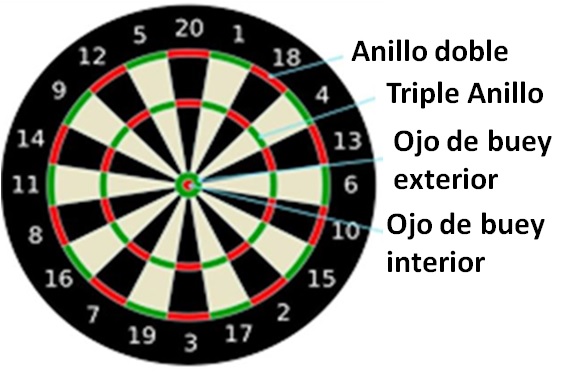
Sara: ¿Podemos decir que la diana exterior es un círculo con el radio más pequeño?
Priya: si El círculo con el siguiente radio más grande es el anillo triple. El radio más grande es para el anillo doble.
Sara: Eso es genial. Entonces podemos definir las posiciones de los anillos como sus radios con la diana interior como origen.
Priya: Está bien, pero pensé que acababa de hacer eso.
Sara: Sí, pero ahora les mostraré el tablero de dardos con un dardo. Saqué los números de puntuación de este tablero de dardos. Ahora, dime la posición del pasador del dardo.
Priya: Está en el anillo exterior directamente encima de la diana interior.
Sara: Exacto. Ahora me dijiste la posición del dardo. Si podemos escribir Este, Oeste, Norte y Sur, puedes decirme la posición del dardo de una manera más precisa.
Priya: Sí, ahora puedo decir que el pasador del dardo está al norte del centro de la diana interior.

Sara: Si pongo el dardo en algún lugar que no esté exactamente en ninguna de las direcciones escritas allí pero en un ángulo diferente, será más difícil que me digas la posición del dardo.
Priya: ¿No podemos escribir posiciones de diferentes ángulos para hacerlo más fácil?
Un papel cuadriculado con coordenadas polares.
Sara: Sí, podemos. Acabas de pedirme un papel cuadriculado con coordenadas polares.
Priya: ¿Lo hice? Ni siquiera sé qué son.

Sara: Las coordenadas polares te dicen la distancia desde el origen y el ángulo donde está un punto. El ángulo comienza en el Este como 0° y luego va hacia el Norte como 90°, hacia el Oeste como 180° y hacia el Sur como 270°.
Priya: Eso está bien. Si el dardo estuviera en cualquier parte de este gráfico, podría haber dicho exactamente dónde estaba: a qué distancia del origen y en qué ángulo.
Sara: Las coordenadas del dardo se escribirían como: r, θ donde r es la distancia desde el origen y θ es la ubicación angular. En los libros, también verá la palabra módulo para r y argumento para θ.
Priya: ¿Cuál es el problema de las coordenadas polares sobre las coordenadas regulares x, y (cartesianas) que aprendimos en geometría? ¿Se pueden convertir entre sí?
Sara: Ambos se utilizan para diferentes propósitos. Las coordenadas polares se usan más en geografía porque la tierra es algo así como una esfera. También se utilizan en navegación, para radares y en cualquier otro lugar donde se desee comprender las curvas. Sí, puede convertir coordenadas cartesianas en polares y también coordenadas polares en cartesianas usando trigonometría.
Mapa de Priya en coordenadas polares
Por ahora, trabajemos para mejorar la puntuación de su proyecto. Quiero que superpongas las coordenadas polares en el mapa que me mostraste antes. Pon tu tienda en el origen.
Priya: A partir de la imagen en coordenadas polares, veo que la mayoría de nuestros clientes provienen de θ = 90° a 360°, que está marcado aquí como 0°. Hay muy pocos clientes de θ = 0° a 90°. En θ = 90° a 360°, más clientes vienen de cerca y menos de lejos. No sé cómo decir mejor esta parte.

Sara: Para la segunda parte puedes decir: “Existe una relación inversa entre la distancia y la cantidad de clientes”. Ahora tenemos que decir por qué hay muy pocos clientes de θ = 0° a 90°. Esto se debe a que hay un río que corre muy cerca de tu tienda en ese lugar. ¿Qué ubicación crees que sería la mejor para tu tienda si pudieras moverla?
Recomendaciones basadas en el estudio
Priya: Una tienda cerca del puente pero del mismo lado será la mejor ubicación porque entonces nuestros clientes actuales seguirán cerca y seguirán viniendo y también obtendremos más clientes del otro lado del río. Creo que si es posible y podemos permitírnoslo, esa ubicación sería genial.
Sara: Ahora, escribe todas las observaciones y recomendaciones en tu informe. Además, ¿cuál es el título de su informe?
Priya pensó por un momento y luego dijo: “El efecto de los factores geográficos en el éxito de un negocio”.
Priya reescribió el informe basándose en lo que había discutido con Sara. Le entregó el informe al profesor de Geografía y también le dio una copia a su mamá.
Priya obtuvo el 100% en el informe. Ella estaba muy feliz. Esta fue la primera vez que obtuvo el 100% en cualquier tarea o prueba. Mamá también se alegró de ver el gran trabajo que había hecho Priya. Ella le había dado una sugerencia real para mejorar el negocio.
Priya vino a visitar a Sara y le dio la emocionante noticia de que estaba al 100 % en el proyecto. Dio las gracias a Sara por toda su ayuda. Como muestra de agradecimiento, su mamá le dijo que le diera a Sara dos cupones para camisetas: tal vez uno para Sara y otro para su novio.
Sara: Gracias, pero no tenías que hacer eso. Me encantó trabajar contigo. Así es como llegué a aprender sobre las coordenadas polares yo mismo. Priya se despidió de su nuevo amigo y se fue.
Desafío
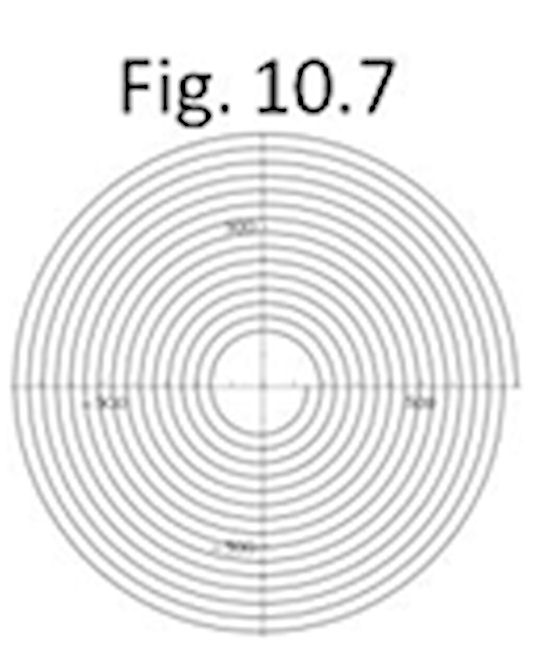
Priya le contó a su hermano Joga, de 14 años, cómo usó las coordenadas polares para obtener el 100 por ciento en su tarea de geografía. Joga, le dijo a Priya: “Gracias por la idea, me vendría bien”. Se suponía que Joga debía cortar el césped. Así que fue al patio. En medio del patio, clavó en el suelo una gran estaca de madera con un radio de 7 centímetros. Estiró completamente el otro extremo de la cuerda y ató una cortadora de césped que ahora estaba a 8 metros del centro de la estaca. Después de que encendió el cortacésped en piloto automático, comenzó a moverse alrededor de la clavija. La cuerda ahora se enrollaba alrededor de la clavija. Luego llamó a Priya y le dijo: “Mira las coordenadas polares. Ahora, dibuja el camino de la cortadora de césped”. ¿Cómo crees que se veía el boceto de Priya?
Solución: La clavija tiene un radio (r) de 7 cm. La circunferencia de un círculo es 2πr o aproximadamente 2 x 22/7. La circunferencia de esta clavija es de unos 7 x 2 x 22/7 o 44 cm. Al principio, el cortacésped está a 8 metros de la clavija. A medida que corta, no puede alejarse, trata de hacer un círculo, pero a medida que gira, la cuerda se enrolla alrededor de la clavija a una velocidad de 44 cm por revolución. El camino se acortará en 2πr con el movimiento de un ángulo de 2π radianes. Si el valor del ángulo θ está en radianes, la trayectoria será una espiral con la ecuación
r = 800 – 7 θ cm. Aquí está el bosquejo del camino de 0 a 30 π radianes, que son 15 vueltas de la espiral.