Triángulos amorosos en el cine.
La Sra. Rania Ali enseñó a estudiantes de una escuela primaria ubicada en un barrio pobre. Los niños tenían muy poco interés en aprender, la Sra. Ali estaba consciente de su desafío, pero la gran maestra encontró nuevas formas de llamar la atención de sus alumnos. Este fue otro día interesante.
Dos niñas, Mehak y Arisha, estaban sentadas en la clase, charlando y riéndose. La Sra. Ali les preguntó por qué estaban hablando en clase y qué era tan interesante y divertido. Las chicas no respondieron a este comentario, tal vez estaban asustadas. Rehan, un chico sentado cerca respondió en su lugar. Le dijo a la Sra. Ali que los dos estaban hablando sobre un triángulo amoroso en un drama en serie que vieron anoche.
Sra. Ali: Mehak, Arisha y Rehan, los tres pasan al frente.
Rehan: Pero, ¿por qué yo, Sra. Ali? yo no estaba hablando
Sra. Ali: Los escuchaste con suficiente atención. Así que los tres pasan al frente y se enfrentan a la clase. Les dijo que formaran un triángulo.
Triángulos escaleno, isósceles y equilátero
Toda la clase se reía porque pensaban que se trataba de otro triángulo amoroso.

Sra. Ali: Clase, dejen de reírse. Los tres te van a enseñar sobre diferentes tipos de triángulos. Ves alguna relación en la distancia entre Mehak y Arisha, Arisha y Rehan o Rehan y Mehak.
Uno de los estudiantes dijo que las tres distancias eran diferentes entre sí.
Sra. Ali: Un triángulo en el que los tres lados son diferentes se llama triángulo escaleno. Ahora, quiero que ustedes tres formen un triángulo en el que Rehan esté a la misma distancia de Mehak que él de Arisha. Este tipo de triángulo en el que dos lados tienen la misma longitud se llama triángulo isósceles. Note que el ángulo Rehan-Mehak-Arisha es el mismo que Rehan-Arisha-Mehak. Esta es una propiedad de un triángulo isósceles que los ángulos opuestos a los lados iguales también son iguales.
Los tres estaban inquietos cuando les dijo a Arisha y Mehak que se movieran para que la distancia entre cada par de estudiantes fuera la misma. Este era un triángulo equilátero y los tres ángulos también eran iguales en él.
Triángulos ….. clasificados por sus ángulos
Rajab: Sra. Ali, mi hermano me dijo que los triángulos se clasificaban según sus ángulos. Sra. Ali: Tu hermano tenía razón. También puedes clasificar los triángulos según sus ángulos. Los dibujaré en la pizarra. Si uno de los ángulos de un triángulo es de 90°, se llama triángulo rectángulo. En esta imagen, el triángulo de ángulo recto está en el medio.

Rajab: El triángulo de la izquierda es un poco obeso, ¿es por eso que se llama obtuso?
Sra. Ali: Eso es divertido Rajab. En el triángulo de la izquierda, un ángulo mide más de 90° y por eso se llama triángulo obtuso. El de la derecha tiene todos los ángulos menores de 90° y se llama triángulo acutángulo.
Algunas chicas en la parte de atrás estaban susurrando un lindo triángulo cuando escucharon la palabra agudo. De repente, Taheen levantó la mano.
Sra. Ali: Taheen, ¿por qué tienes la mano levantada?
Taheen: Dijiste que no podía dibujar en las paredes de la escuela. ¿Puedo dibujar algo en una pizarra? Es solo un montón de líneas.
Sra. Ali: Está bien, Taheen, pero será mejor que sea bueno.
Taheen acaba de hacer un boceto en la pizarra.

Sra. Ali: ¿Qué dibujaste Taheen?
Taheen: No lo sé. Solo pensé que se vería bien. Así que lo dibujé.
Sra. Ali: Esta es una imagen de un triángulo con los brazos extendidos hacia afuera. Forma tres ángulos dentro del triángulo. Los marcaré en negro como los ángulos interiores del triángulo. También hace tres ángulos exteriores como los marqué en rojo.
La Sra. Ali hizo una pausa por unos segundos y luego dijo: Te iba a enseñar la siguiente parte otro día, pero lo haré ahora porque Taheen hizo este dibujo. Aquí está. La suma de todos los ángulos exteriores de un triángulo es 360°.
Taheen: Si hubiera dibujado un cuadrado, ¿la suma de los ángulos exteriores seguiría siendo 360°?
Sra. Ali: Podrías dibujar una figura con 3,4,5,6 o cualquier número de lados, la suma de los ángulos exteriores siempre será la misma: 360°.
Rajab: Sra. Ali, veo que la imagen se basa en tres líneas rectas. En cada recta la suma de los ángulos exterior e interior será 180°. Entonces los tres ángulos interiores y los tres exteriores sumarán 540°. ¿Significa eso que la suma de los tres ángulos interiores de un triángulo siempre será 180° porque 180 más 360 es 540?
Sra. Ali: Clase, ¿qué estoy haciendo aquí? Taheen presenta un boceto para enseñar y luego Rajab presenta el siguiente teorema: la suma de todos los ángulos interiores de un triángulo es 180°.
Mehak: Lamento que estuviéramos charlando en la parte de atrás al comienzo de la clase. Quiero compensar agregando algo, espero que sea correcto. Un triángulo no puede tener más de un ángulo recto.
Sra. Ali: ¿Qué te hace decir eso?
Mehak: Porque dos ángulos rectos ya sumarán 180° y luego el tercer ángulo tendrá que ser cero.
Arisha: Ella tiene razón. También un triángulo obtuso puede tener solo un ángulo mayor a 90°.
Sra. Ali: Eso es genial Mehak y Arisha. Estabas prestando atención en la clase. Te perdono por charlar al principio de la clase pero no lo vuelvas a hacer.
El genio de Rajab
Rajab fue a la oficina de la Sra. Ali después e hizo una pregunta. ¿Tendría razón si dijera que la suma de todos los ángulos internos de una figura de n lados será (n x180°) – 360°? Como para un cuadrado n =4, entonces la suma de todos los ángulos interiores será 360°.
Sra. Ali: Eres un genio Rajab. Nunca lo había pensado de esa manera, pero es correcto.
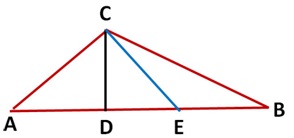
Desafío
CD es perpendicular a AB, y las líneas AC y CE tienen la misma longitud. Identifica todos los triángulos agudos, de ángulo recto, obtusos, escualeno, isósceles y equiláteros en esta imagen. Tenga en cuenta que puede tener ninguno, uno o más de cualquier tipo. No se proporcionó ninguna solución para este desafío.