
(Hay varios lugares con este nombre, pero esta historia trata sobre Connaught Place en Nueva Delhi, India)
Sobre el primer viaje a Connaught Place
Tanya, una chica inteligente de 16 años de Patna ha venido a pasar las vacaciones de Dussehra con su tía materna en Delhi. La tía tiene un hijo, Adi, que tiene aproximadamente la misma edad que Tanya. Tanya lo trata como a su hermano y le envía rakhi todos los años. A pedido de Tanya, la llevó a visitar Connaught Place con la condición de que lo ayudara a aprender trigonometría. De todos modos, ambos fueron a Connaught Place y ahora toda la familia está sentada para tomar el té por la noche.
Papá de Adi: Tanya, cuéntanos cómo te gustó Connaught Place.
Mamá de Adi: Cuéntenos en detalle a dónde fueron, qué comieron y qué compraron.
Tanya: Connaught Place un lugar interesante. Salimos de Metro y nos dirigimos hacia Odeon Sweet House, y de allí caminamos por Connaught Circus hacia el norte, hasta Radial Road 4. Luego caminamos hasta Janpath donde compré algunos recuerdos para mis amigos. en Patna. Después de eso fuimos a un café y luego de regreso a Central Park y tomamos Metro de regreso a casa.
Adi: Ella también me compró una camisa. Ella me enseñó trigonometría cuando estuvimos allí y más después de que volvimos a casa. Papá, todo se me pasó por la cabeza cuando enseñaban Trigonometría en la escuela y en el centro de instrucción. Cuando Tanya lo enseñó, encontré que el tema era muy fácil y todo tenía sentido. Si Tanya me enseña un poco más, puedo dejar el centro de enseñanza para siempre.
Papá de Adi: ¡En serio!
Tanya: Tío, creo que Connaught Place se construyó para enseñar Trigonometría: sus tres círculos concéntricos y sus calles radiales cuidadosamente diseñadas lo atestiguan. Ya sabes, nos vamos mañana otra vez.
Connaught Place otra vez
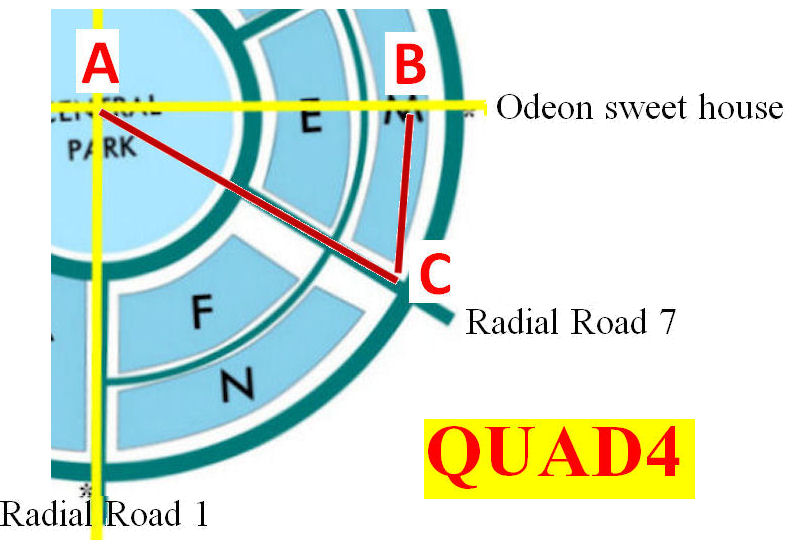
A la mañana siguiente, la mamá de Adi llenó sus estómagos, después de lo cual Adi y Tanya se fueron de casa. Cogieron el metro y llegaron a Connaught Place. Pasearon por Central Park por un rato y luego Tanya encendió la aplicación en su teléfono inteligente. De esta manera, sabrían cuánto se mueven en una dirección determinada. Ella le dijo a Adi que hoy debería seguir observando las distancias recorridas usando este teléfono inteligente. Como ayer, caminaron hacia el este hasta llegar a Connaught Circus y Odeon Sweet House (ver foto).

Adi: Nos hemos movido 350 metros hacia el Este y cero hacia el Norte.
Ambos siguieron caminando en sentido contrario a las agujas del reloj en Connaught Circus mientras charlaban y miraban a su alrededor. Lentamente, llegaron a Radial Road 4, que está al norte de Connaught Circus. En el camino hacia allí, Adi había verificado en el teléfono celular que la distancia en la que se movían hacia el Este había ido disminuyendo gradualmente, mientras que para el movimiento hacia el Norte había ido aumentando.

Adi: Ahora, hemos llegado a Radial Road 4. Nuestro movimiento hacia el norte es de 350 metros y nuestro movimiento hacia el este se ha vuelto cero. Veamos qué pasa después. Mierda, parece que algo anda mal con el teléfono celular. Ahora la distancia recorrida hacia el norte está disminuyendo y, lo que es peor, la distancia recorrida hacia el este es negativa.

Tanya: No hay nada malo con el teléfono celular y esperaba que esto sucediera. En Connaught Circus, fuimos lo más al norte que pudimos en este círculo. Ahora vamos hacia el Sur, por lo que la distancia recorrida hacia el Norte disminuye. Adi, ¿recuerdas cuando hicimos los ejes X e Y en un papel cuadriculado? El eje vertical era Y y el eje horizontal era X. Hemos subido lo más alto posible en el eje Y y bajaremos ahora. Además, ¿recuerdas que los valores de los puntos del eje X a la derecha del eje Y eran positivos y los que estaban a su izquierda eran negativos (ver esta imagen)? Mira, he hecho cuatro cuadrantes (quads) en esta imagen. El primer cuadrante es de 0° a 90°, el segundo es de 90° a 180°, el tercero es de 180° a 270° y el cuarto es de 270° a 360°. También podemos decir que los valores de X e Y son positivos en el primer cuadrante pero en el segundo cuadrante los de X son negativos. Entonces, después de una rotación de 90° en un círculo, en el segundo cuadrante comenzamos a ir hacia el Oeste, lo cual es negativo de ir hacia el Este.

Adi siguió caminando por Connaught Circus. La distancia recorrida hacia el norte desde el punto de partida siguió disminuyendo y el valor negativo del movimiento hacia el este siguió aumentando. Luego cruzaron Shahid Bhagat Singh Marg, que es el punto más occidental de Connaught Circus. Eso significaba que habían entrado en el tercer quad. Siguió adelante y llegó al cuarto quad cuando cruzaron la Radial Road 1. En ese momento estaba confundido y no prestaba mucha atención, pero la aplicación todavía estaba encendida y grabando. Siguieron moviéndose hasta el punto de partida: la dulce casa de Odeon.
Adi: Tanya, entiendo un poco los movimientos, pero ¿qué tienen que ver con Trig?
Tanya: Entenderás todo en casa. Por ahora, quiero un poco de helado.
Encontraron una heladería, comieron un helado y se fueron a casa.
En casa, Tanya hizo un boceto y luego llamó a Adi.
Tanya: ¿Recuerdas que en álgebra hicimos ejes horizontales y verticales? Los valores en el eje horizontal fueron positivos en el lado derecho del eje vertical y negativos en el lado izquierdo. De la misma manera en el eje vertical los valores fueron positivos arriba del eje horizontal y negativos abajo.
Los cuatro cuadrantes y los ejes X-Y
Adi: Tanya, incluso hiciste cuatro cuadriláteros y un triángulo rectángulo en cada cuadrilátero. La hipotenusa en cada triángulo mide 350 metros. De esa manera∠BAC = 30°, ∠BAE = 150°. ∠BAF = 210° y ∠BAG = 330°.
Tanya: Ahora determina los valores de las funciones trigonométricas de estos ángulos.
Adi: sen BAC = 0,5, sen BAE = 0,5, sen BAF = – 0,5 y sen BAG = -0,5. cos BAC = 0,866, cos BAE = -0,866, cos BAF = -0,866 y cos BAG = 0,866. tan BAC = 0,577, tan BAE = – 0,577, tan BAF = 0,577 y tan BAG = – 0,577. Recordé los valores para los del primer quad de ayer, el resto solo cambié los signos en base a lo que me dijiste. Todos fueron positivos en el primer quad, solo sen fue positivo en el segundo, tan en el tercero y cos en el cuarto. Ahora entiendo lo que intentabas ver en Connaught Place. Es interesante pero no sé cómo los memorizaré.
Tanya: Mi papá me enseñó “cine después de la escuela” o “chocolates después de la escuela o “tazas de té con cuchara”. Memoriza lo que quieras. Me gustan los chocolates. Una cosa más.
En el trabajo profesional, los ángulos generalmente se miden en radianes en lugar de grados. El principio es que se necesitan 2π radianes o 360° para completar la vuelta de un círculo. Recuerda que aprendimos que la razón de la circunferencia de un círculo a su diámetro es π. π es aproximadamente 22/7. Por lo tanto, un radián es aproximadamente 360°/ 2π ≈ 57°. En este sistema el primer cuadrilátero es 0 a π/2, el segundo de π/2 a π, el tercero de π a 3π/2 y el cuarto cuadrilátero es 3π/2 a 2π.

Puede ser que esta lección haya sido difícil para Adi. Aún así, Tanya le dio gráficos para los valores de sen x, cos x y de 0 a tan x de 0 a 2π.
Adi notó que los valores de sen x y cos x en las gráficas oscilaban solo entre 0 y 1. Eso tenía sentido porque la altura o la base de un triángulo rectángulo no puede exceder la longitud de su hipotenusa. Además, fue interesante que sen x fuera positivo solo en los dos primeros cuadrantes y cos x en el primero y cuarto. También notó que cos x decrecía con el aumento de sen x. Eso también tenía sentido porque sin2x + cos2x =1 o sin2x = 1 – cos2x.
El más intrigante fue el gráfico de tan x. No se detuvo en uno como lo hicieron los gráficos sen x y cos x, sino que siguió aumentando en su valor. Además, fue positivo justo antes de los 90°, y de repente tomó un valor negativo muy grande. Lo mismo sucedió alrededor de los 270°. Le recordó a un chico que estaría extremadamente feliz en un momento y luego, de repente, comenzaría a llorar.
Adi se mantuvo ocupado con el libro Trigonometría. Esta seguridad fue suficiente de que Tanya ayudaría con algo si fuera necesario. Después de dos días, Tanya regresó a Patna.
Después de un mes, Adi le envió una foto por teléfono. Era el resultado de su prueba Trig en la que había obtenido un 100 %. No sabemos a quién le mostró Tanya esta foto: para decir lo inteligente que era su hermano o para decir lo inteligente que ella lo había hecho. Pues tú decides.
Desafío
Tanya ve trigonometría en todo. Mira lo que hizo ahora, le dio a Adi una foto de Qutab Minar y le dijo que tiene una altura de 93 metros. Trazó una línea recta AC hacia abajo a lo largo de la pared y luego dibujó una línea AB vertical al suelo. Trazó una línea que conecta B y C y dijo que tenía 5,8 metros de largo. Luego le hizo dos preguntas. Uno era la longitud de la pared de arriba a abajo y el segundo era la medida del ángulo BCA. ¿Puedes resolver esto?

Responder
La longitud del muro según el teorema de Pitágoras será √(932+5,82) = 93,18 metros.
Ahora tan BCA = 93/5.8. Por lo tanto, el ángulo BCA = arctan (93/5.8) = arctan 16.03 que es 86.43° (Tomado de Internet).