Happy Sr. Power significó una lección exigente
El Sr. John Power parecía muy feliz de nuevo. Muchos estudiantes comenzaron a pensar que debe tener algo bajo la manga. La última clase, vino con la misma cara feliz, le había pedido a la clase que determinara el valor de pi usando trigonometría. Todos se preguntaban qué se le había ocurrido esta vez.
Sr. Power: Hoy vamos a aprender sobre triángulos rectos, obtusos y agudos. Tinku, ¿qué es un triángulo rectángulo?
A Tinku le divirtió lo fácil que era esta pregunta y espetó: Un ángulo recto es un triángulo en el que uno de los ángulos es un ángulo recto de 90°.
Sr. Power: ¿Quién puede decirme qué son los triángulos obtusos y agudos?
Varios estudiantes levantaron la mano pero el Sr. Power le preguntó a Tracy.
Tracy: En un triángulo obtuso, uno de los ángulos mide más de 90°, pero en un triángulo agudo, los tres ángulos miden menos de 90°.
Clasificando triángulos basados en cosenos
Sr. Power: Sara, escribe las funciones trigonométricas de los tres tipos de triángulos.

Sara fue a la pizarra e hizo esta tabla para el ángulo más grande (BAC) en cada tipo de triángulo (ver Figura).
| Obtuso | Ángulo recto | Aguda | |
| Sin BAC | >0 pero< 1 | 1 | >0 pero < 1 |
| Cos BAC | <0 (negativa) | 0 | >0 pero < 1 |
| Tan BAC | <0 (negativa) | ∞ | >0 pero< ∞ |
Sr. Power: Buen trabajo Sara. Ahora bien, si tuviera que definir los tres tipos de triángulos en función de las relaciones trigonométricas, ¿qué función elegiría?
Sara: Porque, porque es simple: negativo para obtuso, 0 para ángulo recto y positivo para triángulo de ángulo agudo.
Muchos estudiantes estaban asombrados de cómo se podía usar la trigonometría para definir los tres tipos de triángulos.
Clasificación algebraica
Sr. Power aún no había terminado. Preguntó si alguien recordaba el Teorema de Pitágoras que habían aprendido en Geometría. Muchos estudiantes levantaron la mano y él llamó a una estudiante llamada Tracy para que describiera el teorema.
Tracy: En un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados.
Sr. Power: Si la longitud de la hipotenusa es c y los otros lados tienen longitudes a y b, ¿diría que entonces c2 = a2 + b2?
Tracy: Sí, Sr. Power.
¿Funciona c2 = a2 + b2 para triángulos obtusos?

Sr. Power: Muy bien, clase. Quiero que se sienten en grupos de tres y averigüen si esta relación también se aplicará a los triángulos de ángulo obtuso con la longitud del lado más largo siendo c y los otros dos lados siendo a y b. Te dare una pista. En los triángulos ABC de la pizarra, traza una línea vertical desde la esquina C hasta la base AB.
Para un triángulo obtuso ABC, la longitud del lado BC opuesto al ángulo obtuso es c, la base AB es a y el lado AC es b. Dibujamos una línea vertical CD que llegaba a la base extendida AB en D. Sea h la longitud de BD y x sea AD.
Luego, del gran triángulo rectángulo DCB, h2 = c2 – (a+x)2.
Del triángulo DAC, h2 = b2 – x2.
Por lo tanto c2 – (a+x)2 = b2 – x2.
Sumando (a+x)2 a ambos lados de la ecuación, obtenemos c2 = (a+x)2 + b2 -x2 que es
c2 = a2+2ax +x2 + b2 -x2 o c2 = a2 + b2 +2ax.
Porque a, b, c y x son todos positivos c2 > a2 + b2.
El Sr. Power junto con la mayoría de los estudiantes aceptaron la prueba y quedaron impresionados.
Describir tipos de triángulos con ecuaciones algebraicas
Sr. Power: Bien hecho, Tommy y sus compañeros Sara y Johnny por demostrar que en un triángulo obtuso c2 > a2 + b2.
Recuerda que Tracy dijo que para un triángulo rectángulo c2 = a2 + b2. Voy a agregar que para un triángulo de ángulo agudo con el lado más largo de longitud c, c2 < a2 + b2y tu tarea es demostrarlo.
Para los triángulos obtuso, rectángulo y acutángulo, el cos del ángulo opuesto a los lados mayores será negativo, 0 y positivo, respectivamente. Voy a agregar que podríamos escribir que c2 > a2 + b2, c2 = a2 + b2 y c2 < a2 + b2, respectivamente. Aquí está el resumen de la lección de hoy.
| Obtuso | Ángulo recto | Aguda | |
| Cos BAC | <0 (negativa) | 0 | >0 pero < 1 |
| Valor del lado más largo c | c2 > a2 + b2 | c2 = a2 + b2 | c2 < a2 + b2 |
Desafío
Demostrar que para un triángulo agudo con lados de longitud a, b y c y el lado más largo de longitud c, c2 < a2 + b2.
Solución:
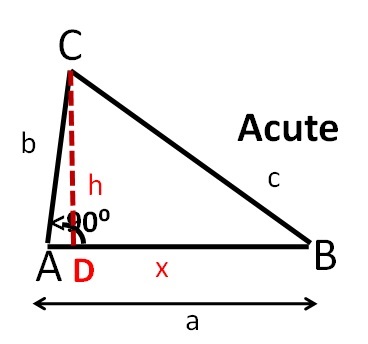
Dado: Un triángulo acutángulo ABC, el lado BC es el lado más largo de longitud c y la longitud del lado AB = a y AC = b.
Dibuje una línea vertical BD que se una a la base en D. Sea h la longitud de BD y x, luego AD de longitud = a-x.
Del triángulo rectángulo BCD, c2 = h2 + x2
Del triángulo rectángulo ACD, b2 = h2 + (a-x)2 o h2 = b2 – (a-x)2
Por lo tanto c2 = b2 – (a-x)2 + x2 o c2 = b2 + x2 – a2 – x2 +2ax
x2 o c2 = b2 – a2 +2ax o c2 = b2 + a2 – 2a2 +2ax o
c2 = b2 + a2 – 2a (a – x)
Como a es mayor que x, a-x son positivos y, por lo tanto,
c2 < (a2 + b2).