
(Hay varios lugares con este nombre, pero esta historia trata sobre Connaught Place en Nueva Delhi, India)
Connaught Place un centro económico y de negocios
Connaught Place es probablemente el mayor centro económico y comercial de Delhi, la capital de la India. No solo eso, los turistas indios y extranjeros encuentran que esta es una de las mayores atracciones de esta ciudad. Para los visitantes de Europa y América es un mercado cómodo. Eso sí, los estudiantes universitarios y de secundaria también disfrutan de roaming aquí. Esta zona se construyó en la época en que los gobernantes británicos trasladaron la capital india de Calcuta a Nueva Delhi. Alrededor de esta área, particularmente al sur, se encuentran las mansiones que fueron construidas para los oficiales británicos y luego para los reyes de las colonias indias. Connaught Place se construyó como un elegante mercado para ellos. Más al sur se encuentran los centros legislativos y administrativos de la capital.
El sello distintivo de Connaught Place es la aparición de un gran círculo
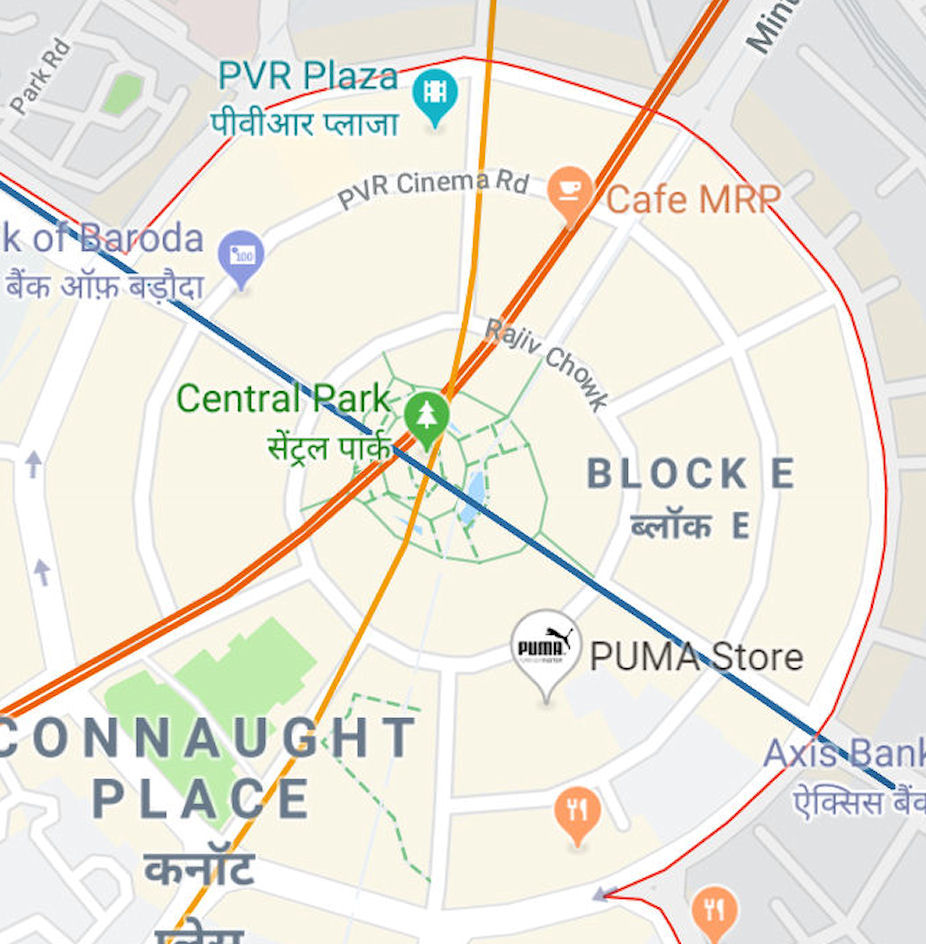
En la Delhi de hoy, Connaught Place está en el centro o algo al este del centro de la ciudad. Está rodeado por importantes áreas de población en todas las direcciones. El sello distintivo de Connaught Place es la apariencia de un gran círculo desde el cual los caminos se extienden en diferentes direcciones. El diseño principal de esta área son tres círculos concéntricos. En el medio está Center Park, que tiene lugares para que la gente se siente y disfrute del paisaje. Este parque ha sido utilizado para varios tipos de reuniones. Este parque de 150 metros de radio está rodeado por una carretera denominada Inner Circle. A unos 100 metros de esta carretera se encuentra Middle Circle y a otros 100 metros se encuentra la carretera exterior que se denomina Connaught Circuit. Las carreteras radiales numeradas del 1 al 7 y Parliament Street salen del circuito de Connaught. Entre las diferentes calles hay tiendas, restaurantes y cafeterías, bancos, hoteles, cines, etcétera. Una vista aérea de esta área muestra una simetría distinta. Y sí, hay muchos sitios dignos de ver en el este y el sur de esta zona. Atraído por la belleza de esta zona, Bollywood también la ha utilizado para filmar. Hay varios medios de transporte para llegar a esta zona. No es de extrañar que Connaught Place esté abarrotado todo el tiempo.
Tanya y Adi
Tanya es una chica de 16 años que vive en Patna, India. Es hija única de sus padres y ha venido a Delhi a visitar a su mausi (hermana de la madre). Esta es la primera vez que realiza un viaje sin acompañante a Delhi. La última vez que vino a Delhi fue hace 6 años, cuando solo tenía diez años, y vino aquí con su madre. Mausi tiene un hijo Adi que tiene la misma edad que Tanya. Tanya envía rakhi a Adi y lo trata como a su hermano (un ritual simbólico que une a un hermano y una hermana). De vez en cuando los dos también hablan por teléfono. Cuando llegó a Delhi, Tanya sabía que tendría su compañía. Los dos estaban sentados y charlando sobre lo que sea, tu suposición es tan buena como la mía.
Tanya: Aún no he visto Connaught Place. Un amigo mío de Patna lo vio y dijo que mola, un lugar de visita obligada. ¿Puedes llevarme mañana a verlo, por favor bonita por favor?
Adi: Es difícil. Soy débil en Matemáticas y todos los días voy a una universidad de matrícula. Tengo que hacer tarea desde allí también. Mi mamá no me dará permiso para holgazanear así.
Tanya: Te conseguiré el permiso. Soy la sobrina favorita de tu papá. Bajo mi persuasión, te pedirá que lo hagas. Por cierto, ¿qué materia de Matemáticas es el curso para el que vas al centro de matrícula?
Adi: Trigonometría, todo pasa por encima de mi cabeza.
Tanya: Adi, en ese caso pon una sonrisa en tu rostro. Haré de ti un genio en Trigonometría que enseñarás a tus amigos. Ni siquiera tendrás que ir al centro de matrícula. Solo que mañana y pasado tendrás que venir conmigo y mostrarme Connaught Place. No te asustes, te conseguiré el permiso y también tengo algo de dinero, mi papá me dio algo para el viaje.
Fiel a sus palabras, Tanya se dirigió al padre de Adi: Tío, ¿qué está pasando aquí? ¿Por qué estás torturando a mi hermano Adi enviándolo a la escuela de matrícula? Fácilmente puedo enseñarle trigonometría muy bien, algo de vez en cuando por Skype desde Patna. Sácalo de este sufrimiento y dile que pase los próximos cuatro días conmigo, su hermana. Me puede llevar a ver lugares en Delhi. Su mente se refrescará y también ahorrará la tarifa del centro de matrícula.
Eso fue todo lo que tomó. El papá de Adi sabía que Tanya sacaba notas casi perfectas en todas las materias. Pensó que Adi podría aprender algo estando en su compañía. Fue a su hijo: Adi, tu hermana ha venido después de 6 años. No sé cuándo vendrá de nuevo. Hablar con ella. Aquí hay algo de dinero. Llévala a ver lugares de la ciudad. Puede tomarse unos días libres de la escuela de matrícula.
Adi le dijo que sí a su papá, puso el dinero en su bolsillo y luego habló con Tanya: Oye, hermana, ¿qué tipo de magia usaste con mi papá? Casi me ordena que te lleve para mostrarte Delhi, e incluso me dio algo de dinero para los gastos. Está bien, dime una cosa. ¿Qué te hizo sentir tan seguro de decir que podrías convertirme en un genio en trigonometría?
Tanya: Primero, obtuve una calificación del 100% en este tema, segundo, he ayudado a muchos amigos en eso y tercero, mi querido hermano, solo para ti, instalé una aplicación especial en mi teléfono inteligente. Entonces, ¿a qué hora iremos mañana para visitar Connaught Place?
Connaught Circus es la carretera circular más exterior del área de Connaught Place
A la mañana siguiente, la mamá de Adi llenó sus estómagos, después de lo cual Adi y Tanya se fueron de casa. Cogieron el metro y llegaron a Connaught Place. Pasearon por el área de Central Park por un tiempo y luego caminaron hacia la parte este de Connaught Circus, que es la calle circular más externa. Este lugar estaba cerca de la casa de dulces Odeon. Allí, Tanya sacó su teléfono inteligente.
Adi: ¿Quieres llamar a casa?
Tanya: No, he activado la aplicación de la que te hablé. Utiliza GPS para determinar y registrar nuestra ubicación. A medida que avancemos por Connaught Circus, irá registrando nuestra ubicación y también nos dirá cuánto nos hemos movido hacia el Norte y cuánto hacia el Oeste.
Caminaron mientras conversaban y miraban las escenas a su alrededor. Lentamente mientras caminaban, llegaron a Radial Road 4, que es el norte de Connaught Circus. Había todo tipo de tiendas allí. Tanya comenzó a buscar regalos para sus amigos, pero Adi la detuvo diciendo que podían conseguir los mismos artículos mucho más baratos en Palika Bazar o en JanPath. Caminaron desde allí hasta Janpath. El lugar tenía todo tipo de vendedores. Tanya compró algunas cosas de allí. Ahora que tenían hambre y sed, encontraron un café cercano y tomaron algunos refrescos. Tomaron el metro y regresaron a casa.
La mamá de Adi tenía listo el almuerzo. Comieron mientras charlaban y luego decidieron descansar un rato. ¿Qué descanso? Tanya transfirió todos los datos generados por la aplicación a su computadora portátil y comenzó a jugar con ella. En realidad, estaba analizando los datos, pero para Tanya era solo un juego.
Tania: Adi.
Adi: que?
Tanya: Mira este mapa de Connaught Place.
Adi: Nada nuevo, lo he visto un millón de veces.
El mapa esquemático
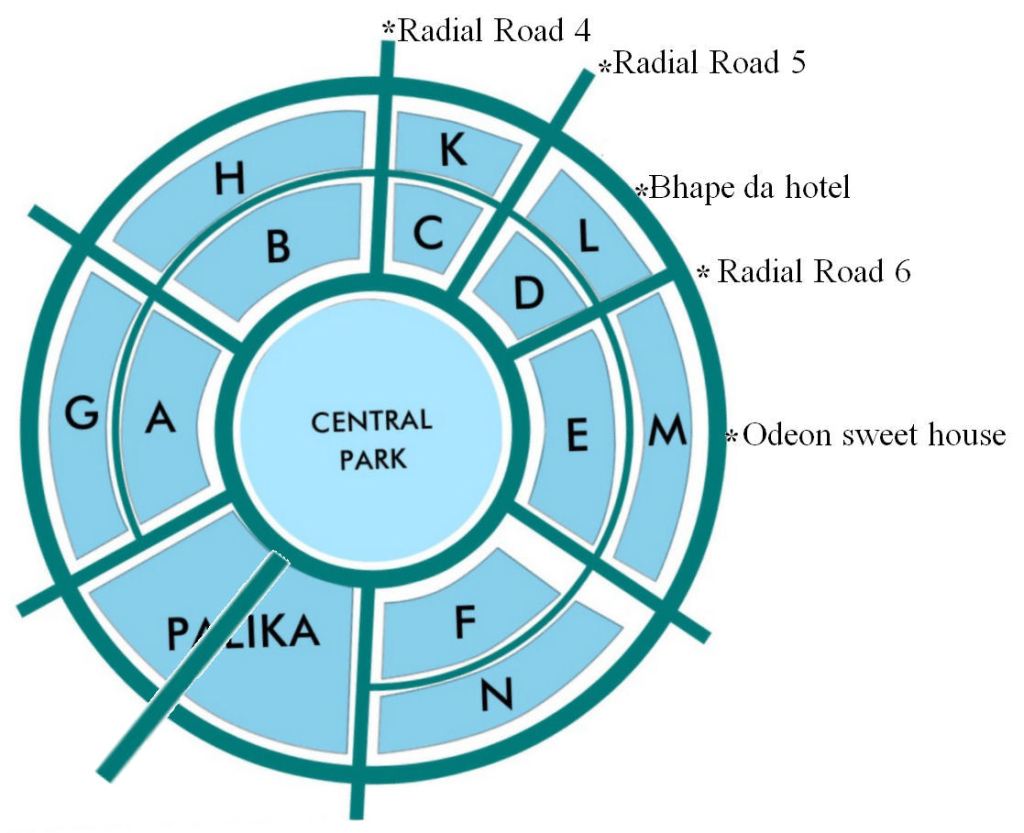
Tanya: Bien, entonces mira este mapa esquemático. Muestra todos los caminos y los edificios. Recuerda, encendí la aplicación en Odeon Sweet House. Eso también lo demuestra. Caminamos en sentido contrario a las agujas del reloj en Connaught Circus y luego en Radial Road 6, Bhape da hotel, Radial Road 5 y Radial Road 4, medí cuánto norte y cuánto oeste habíamos ido desde Odeon Sweet House. Todos estos puntos también se muestran en este mapa esquemático.
Adi: Se ve bien. Qué más ?
La trigonometría se trata de triángulos de ángulo recto
Tanya: La siguiente figura es solo para el área que cubrimos hoy. En esta imagen, se ha dibujado una línea recta AB desde Central Park hasta la casa de dulces Odeon, donde comenzamos a registrar nuestro movimiento. Se ha trazado otra línea AC desde el centro hasta Radial Road 6. Desde C, tengo una línea CB vertical a AB. Debido a que desde Odeon Sweet House hasta Radial Road 4 forma un cuarto de un círculo que es de 90°, y la rotación hasta Road 6 es un tercio de eso, el ángulo BAC es de 30°. Según mi teléfono inteligente, nos habíamos movido 175 metros al norte (línea BC) de Odeon Sweet House. También según este mapa AC es de 350 metros.

Adi: La razón entre la altura de un triángulo rectángulo y su hipotenusa es la función sin, por lo que la razón de las longitudes de CA y AC se llamará sin BAC. Según usted, el pecado BAC es 175/350 o 0.5. Oye, mi calculadora muestra que sin 30° es 0,5. Entonces, ¿cuánto nos hemos movido hacia el oeste según su aplicación?
Tanya: 46,9 metros. Eso significa AB = 350 – 46,9 o 303,1 metros. La razón de las longitudes de la base y la hipotenusa de un triángulo rectángulo es la función cos. Entonces cos (BAC) = 303.1/350 o 0.866.
Adi: Sí, eso es lo que muestra mi calculadora.
Tanya: En realidad, no necesitábamos determinar la longitud de AB de esta manera.
¿Recuerdas el teorema de Pitágoras de la geometría?
Adí: Sí. En un triángulo rectángulo base2 + altura2 = hipotenusa2.
Tanya: Ahora, ¿qué obtendrás si divides ambos lados de esta ecuación por la hipotenusa2?
Adi: altura2/hipotenusa2 + base2/hipotenusa2 = 1. Dios mío, esto significa sin2x + cos2 x = 1. Nadie me lo enseñó así. Ambos, el señor de la escuela y el profesor de matrícula, solo me dijeron la fórmula y me pidieron que la memorizara. Tal vez por eso no se me ocurrió que podría usarlo aquí.
Tanya: Sí, esto también te da cos x = ±√(1 – sin2x). Entonces podemos calcular cos x a partir de sin x. ¿Cuáles son todas las funciones trigonométricas que conoces?
Adi: bronceado, cosec, sec y cot. Altura/base es tan x. cosec x = 1/sin x, sex = 1/cos x y cot x = 1/tan x.
Tanya: Si conoces el valor de cualquiera de las funciones trigonométricas de un ángulo, puedes determinar todas las demás porque todas están relacionadas. Ahora, veamos sin 30° = 0.5. ¿Cuáles serán los valores de todas las demás funciones?
Adí; Hiciste todo tan simple. Como sin 30° = 0,5, cos 30° =√(1 – 0,52) = 0,866, entonces tan 30° = sin 30°/ cos 30° = 0,5/0,866 = 0,577. Todos los demás son recíprocos que se pueden calcular fácilmente con una calculadora.
Adi: Hermana, también has dibujado los triángulos de ángulo recto ADE y AFG en esta imagen, ¿para qué?
Tanya: Sí, quería ver cuánta atención has estado prestando. Dime cuales serian los valores de sin DAE y sin FAG ?
Adi: Independientemente del tamaño de los triángulos, estos ángulos serán de 30° y, por lo tanto, sin DAE y sin FAG serán todos de 0,5. Si me dices las longitudes de la hipotenusa de un triángulo, puedo decirte su altura y base.
Tanya: La hipotenusa del mediano mide 250 metros y la del pequeño 150. No hace falta determinar sus alturas y bases. Solo quería aumentar tu confianza en ti mismo.
Adi: ¿Eso es todo o hay más?

Tanya: Acabamos de empezar. Mira esta segunda foto. Cuando llegamos al hotel Bhape da, habíamos recorrido 247,5 metros al norte. En este triángulo rectángulo ABC, la hipotenusa seguirá siendo la misma que el radio de Connaught Circus, que es de 350 metros. Según mi aplicación, la base de este triángulo también mide 247,5 metros. Ahora dime valores de todas las funciones trigonométricas del ángulo BAC.
Adi: Este es un triángulo isósceles porque AB = BC. Por lo tanto, ángulo BAC = (180° – 90°)/2 = 45°. Por lo tanto,
sin 45° = cos 45° = 247,5/350 = 0,707, tan 45° = 0,707/0,707 = 1
cosec 45° = seg 45° = 350/247,5 = 1,414, cot 45° = 0,707/0,707 = 1
Tanya: Chico Adi, conoces Trigonometría muy bien.
Adi: No, lo que me estás haciendo hacer es geometría que conozco muy bien.

Tanya: Entonces, eres buena en geometría. Trig es lo mismo que geometría, excepto que en lugar de escribir declaraciones largas, solo escribe los valores de las funciones. La relación entre los dos es similar a la que existe entre la aritmética y el álgebra. Bien, haz el último problema de hoy. Cuando llegamos a Radial Road 5, habíamos avanzado 303,1 metros al norte de Odeon Sweet House. Sabiendo esto, determine los valores de todas las funciones de BAC en esta imagen.
Adi: Dado que en ese momento habíamos recorrido dos tercios del primer cuarto de un círculo, ángulo BAC = 60°. AC permanecerá 350 metros. Por lo tanto, sin BAC = 303,1/350 = 0,866. Tanya, ¿puedes comprobar si sin 60° = 0,866?
Tanya: Sí, y eso significa que tenías razón al decir que el ángulo BAC = 60°.
Adi: Gracias Tanya. Ahora, debido a que sin BAC = 0.866, cos BAC = √(1 – sin2 BAC) = 0.5. El bronceado BAC = 0.866/0.5 = 1.732. ¿Debo determinar también los recíprocos de estas tres funciones?
Tanya: No, es suficiente por hoy. Iremos a Connaught Place mañana nuevamente y luego haremos más. Por ahora, vamos a chatear con todos. Tal vez de esa manera conseguiremos un poco de té.
Adi: Tanya, también has puesto una estrella de Radial Road 4. No puedes hacer un triángulo a partir de ahí o hacer uno con base cero pero la misma altura que la hipotenusa. Entonces, ¿diremos que sin 90° = 1, cos 90° = 0 y tan 90° = ∞?
Tanya: Adi, resultaste ser muy inteligente al descubrir todo eso por tu cuenta.
Toda la familia se sentó junta para el té.
Papá de Adi: Tanya, cuéntanos cómo te gustó Connaught Place.
Mamá de Adi: Cuéntenos en detalle adónde fueron, qué comieron y qué compraron.
Tanya: Connaught Place es un lugar interesante. Salimos de Metro y nos dirigimos hacia Odeon Sweet House, y desde allí caminamos por Connaught Circus hacia North hasta Radial Road 4. Luego caminamos hasta Janpath, donde compré algunos recuerdos para mis amigos. en Patna. Después de eso fuimos a un café y luego de regreso a Central Park y luego tomamos Metro de regreso a casa.
Adi: Ella también me compró una camisa. Ella me enseñó Trig cuando estuvimos allí y más después de que volvimos a casa. Papá, todo se me pasa por la cabeza cuando enseñan trigonometría en la escuela y en el centro de matrícula. Pero cuando Tanya lo enseñó, encontré que el tema era muy fácil y todo tenía sentido. Iremos a Connaught Place mañana otra vez.
Desafío
Ramjas School No. 2 en Delhi está en la cima de la montaña Anand Parbat. Muchos estudiantes vienen a esa escuela del lado de Karol Bagh, incluido Munna. Munna llega allí montada en una vieja scooter destartalada. Le dice a su papá que su scooter es como un cacharro. Mientras va por Ghati Road, tiene que caminar 350 metros y arrastrar el scooter porque el camino es demasiado empinado, pero luego la pendiente disminuye y puede volver a andar en scooter. La carretera de Ghati está a 231 metros sobre el nivel del mar cuando comienza, pero después de 350 metros, está a 318 metros sobre el nivel del mar. En lugar de simpatizar con el pobre Munna, el profesor de matemáticas le pide que haga todas las funciones trigonométricas de esta escalada.
Responder

Construya un triángulo rectángulo ABC cuya hipotenusa AC sea de 350 metros y la altura BC sea de 318 – 211 = 87 metros. Dibuja una línea horizontal AB como base del triángulo. Ahora, calcule todas las funciones trigonométricas del ángulo BAC.
cos BAC = √(1 – sin2 BAC) = 0,97, sec BAC = 1/0,97 = 1,03
tan BAC = sin BAC/cos BAC = 0,26, cot BAC = 3,89.
El arcoseno es el inverso de la función sin. El ángulo BAC se puede determinar como arcsin 0.25 = 14.45° usando tablas trigonométricas o una calculadora.