
Muñeca babushka
La Sra. Rania Ali enseñó en una escuela ubicada en un barrio pobre. Los niños tenían muy poco interés en aprender. La Sra. Ali era consciente de su desafío, pero la gran maestra encontró nuevas formas de llamar la atención de sus alumnos. Hoy estaba perdida. No supo cómo abordar la siguiente lección de geometría hasta que vio algo en el escritorio del director. Le pidió al director que le prestara la muñeca que estaba en su escritorio. El director estuvo de acuerdo, pero le pidió a la Sra. Ali que se asegurara de devolverlo.
La Sra. Ali vino a la clase y puso la muñeca en la mesa del maestro. Por supuesto, todos los niños y niñas tenían curiosidad de por qué la Sra. Ali traería una muñeca a la clase.
Sra. Ali: Clase, tengo esta muñeca especial para mostrarles. Es posible que algunos de ustedes ya lo hayan visto en la oficina del director. Es una muñeca babushka. Esta muñeca se puede abrir.
Abrió la muñeca Babushka. Dentro había una segunda muñeca. Lo sacó y cerró la primera muñeca. Luego abrió la segunda y sacó una tercera muñeca. Repitió el proceso dos veces más. Dejó las cinco muñecas sobre la mesa. Muchos estudiantes nunca antes habían visto una muñeca babushka y quedaron hipnotizados. A todos en la clase les gustó la exhibición hasta que Barak habló.

¿Semejantes o idénticos?
Barak: Sra. Ali, las cinco muñecas son iguales.
Mehak: No, no lo son. Todos son de diferente tamaño.
Esto siguió a una discusión en clase, y el acuerdo fue que las cinco muñecas eran similares porque tenían la misma forma y diseño. Serían idénticos si fueran todos del mismo tamaño también pero entonces no podrían ir uno dentro del otro.
Sra. Ali: Muy buena clase. Si uno de los muñecos estaba acostado y los otros estaban de pie. ¿Seguirían siendo muñecos similares?
Los estudiantes comenzaron a susurrar, pero luego Taheen se puso de pie y dijo: “Creo que todavía serían similares porque la muñeca solo está acostada. Podría ponerse de pie fácilmente”. La clase estuvo de acuerdo en que la muñeca con una orientación diferente seguiría siendo similar a las otras muñecas.
Ahora, formas y galletas.
Sra. Ali: Aquí hay una foto de diferentes galletas. Cuáles de ellos son similares entre sí. Arisha: Todos tienen formas diferentes. Así que ninguna cookie es similar a otra.
Sra. Ali: Muy bien Arisha. Ahora aquí hay otra imagen de diferentes cookies.

Arisha: Podría darle la vuelta a cualquiera de las galletas y resultarían similares. Las galletas 1 a 6 son del mismo tamaño, pero la 7 y la 8 son más pequeñas pero aún tienen una forma similar.
Sra. Ali: Rehan, has estado callada. Dime si las cookies 1 a 6 son similares y también del mismo tamaño, dirías que son idénticas.
Rehan: Sí, podría voltearlos y apilarlos uno encima del otro. Las cookies 1 a 6 serían todas exactamente iguales.

Sra. Ali: En geometría, diríamos que los triángulos del 1 al 8 son semejantes pero los triángulos del 1 al 6 también son congruentes. Quiero agregar que los conceptos de similitud y congruencia se aplican a todas las formas, no solo a los triángulos. Aquí hay un ejemplo con cuadriláteros. Mehak, dime ¿cuáles de estas figuras son similares y cuáles son congruentes?

Mehak: Sra. Ali, las formas del 1 al 4 son todas cuadradas y, por lo tanto, similares. La forma 2 es congruente con la forma 1 y la forma 4 es congruente con la forma 3. La forma 7 es similar y congruente con la forma 5. Tendría que medirla para asegurarme de que la forma 6 también sea similar a la 5 y la 7.
Taheen: Sra. Ali, ¿sería correcto si dijera que todos los triángulos equiláteros son similares entre sí, todos los cuadrados son similares, todos los pentágonos son similares y así sucesivamente en la medida en que todos los círculos también son similares entre sí?
Sra. Ali: Similar pero no congruente. Estoy impresionado con tu forma de pensar.
Ventaja en la comprensión de la similitud.
Taheen: Gracias, Sra. Ali, pero no entiendo cuál es la gran ventaja de comprender la idea de la similitud.
Sra. Ali: Dibujé dos triángulos similares: el triángulo 1 y el triángulo 2. Son similares porque el ángulo BAC del triángulo 1 es igual a B’A’C’ del triángulo 2, el ángulo ACB es igual al ángulo A’C’B’ y, por lo tanto, el tercer ángulo CBA = C’B’A’. Ahora bien, si la razón de los lados AB del triángulo 1 y A’B’ fuera dos, ¿quién puede decirme la razón de BC a B’C’ y AC a A’C’?
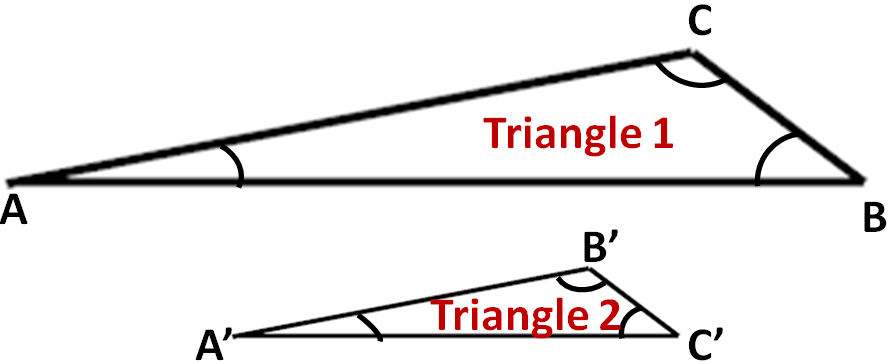
Casi toda la clase levantó la mano, pero la Sra. Ali le preguntó a Feran.
Feran: 2 porque si la razón de cualquiera de los lados fuera diferente en un triángulo, cambiaría su ángulo y los triángulos ya no serían semejantes.
Sra. Ali: Muy bien. Por la cantidad de estudiantes que levantaron la mano, creo que todos entendieron esta idea. Taheen, entonces la ventaja es que no tienes que medir los tres lados, sus proporciones serán las mismas. Aunque usé triángulos para mostrar las proporciones constantes de los lados, la idea se aplica a cualquier forma.
La campana sonó y los estudiantes desaparecieron sin que la Sra. Ali despidiera la clase.
Desafío

ABCD es un cuadrado. Demuestre que AD es perpendicular a BC.
Solución: Dado que ABCD es un cuadrado de lados AB=BD=CD=AC, y CD es paralelo a AB y AC es paralelo a BD.
El triángulo ABD es un triángulo isósceles porque AB = BD. Por lo tanto, los ángulos DAB y ADB son iguales. Los triángulos AEB y DEB son congruentes porque AB = BD (dado), el lado EB es común a ambos y los ángulos DAB y ADB son iguales. Por tanto, ángulo AEB = ángulo BED, pero ángulo AEB = ángulo AEC y ángulo CED y ángulo AEB (ángulos opuestos). Por lo tanto los ángulos AEB = ángulo BED = ángulo DEC = ángulo AEC. Juntos, estos ángulos forman una revolución completa = 360°. Por lo tanto, cada uno de los ángulos es de 90°. Por lo tanto, la línea AD es perpendicular a BC.
Suplementario
ABC es un triángulo rectángulo con ∠ACB siendo un ángulo recto. Dibujar un rectángulo de lado NL paralelo a AC y ML paralelo a AC tal que L toque a AB. Sean los segmentos de línea AN de 7 unidades de largo y BM de 12 unidades. Determinar el área del rectángulo.
Dibuja el triángulo ABC y el rectángulo LMCN como se muestra. Sean los lados del rectángulo CM = ML = a, y CN = ML = b.

Tenga en cuenta que los ángulos en cada esquina del rectángulo son 90⁰.
Dado que los ángulos en una línea recta son 180⁰, ∠ANL = ∠LMB = 90⁰.
AC y LM son paralelos por ser lados opuestos de un rectángulo. Por lo tanto, el ángulo correspondiente ∠NAL = ∠MLB.
De manera similar, ∠ALN = ∠LBM.
Dado que los ángulos correspondientes de ANL y LMB son todos iguales, los triángulos ANL y LMB son similares y sus lados tienen las mismas proporciones.
Por lo tanto, la relación a/7 = 12/b, Ceoss multiplicando los dos lados da ab = 84.
Por lo tanto, el área del rectángulo = ab = 84 unidades.
Determinar el radio de una semicircunferencia inscrita en el lado mayor de un triángulo cuyos lados miden 3, 4 y 5 unidades.
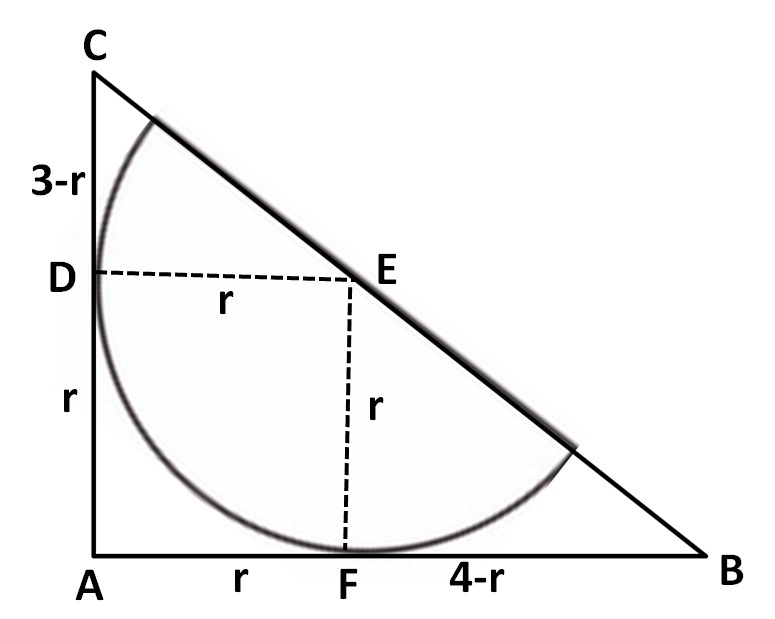
Como las longitudes de los lados son 3, 4 y 5, Pitágoras afirma que es un triángulo rectángulo con la hipotenusa BC porque 52 = 42 + 32, es decir, 25 = 16 +9.
La figura muestra el triángulo ABC y el semicírculo de BC inscrito en él. Dibuja una DE perpendicular desde el centro del círculo en AC y EF en AB.
Sea el radio r. Entonces DE = AF y EF = AD = r. También FB = 4-r y CD = 3-r.
Como DE es paralela a AB, ∠DEC =∠EBF.
Dado que CDE y EFB son triángulos de ángulo recto, ∠BEF también es igual a ∠DCE. Por tanto, estos son triángulos semejantes y sus lados correspondientes tienen las mismas proporciones:
DC/DE = (3-r)/r = EF/FR = r/(4-r).
(3-r)/r = r/(4-r).
La multiplicación cruzada de los dos lados de la ecuación por da:
(3-r)(4-r) = r 2 o 12 + r 2 -7r = r 2 o r = 12/7. Ese es el radio del semicírculo.