
Johnny le guardó un secreto a Sara
Sara está enamorada de Johnny. Llevan saliendo juntos casi cuatro años. Sara y Johnny incluso organizaron una gran fiesta conjunta de graduación de la escuela secundaria para sus amigos cercanos mucho antes del final del año escolar. Se cuentan todo sobre los acontecimientos de su vida, bueno, casi todo. La vida siguió como de costumbre, pero esta fue la única vez que tuvieron una pelea cuando Sara llegó a casa de Johnny después de la escuela y estaban sentados y charlando.
Johnny: Estoy feliz de que me fue muy bien en la escuela, y en gran parte fue gracias a ti. Te dije que mi papá quería que asistiera a XYU y también que obtuve la admisión.
sara: sí, lo sé. También quería ingresar a un programa de ciencias en ZYU y recibí una carta de admisión de ellos la semana pasada. Tú lo sabes. También te dije hace mucho tiempo que Nana me dio algo de dinero y que mis padres han estado poniendo dinero en un fondo de becas. Juntos deberían cubrir al menos el 70% del costo, pero Nana contribuiría si lo necesito. También podría obtener una beca por mérito de la universidad.
Johnny: Sí, me hablaste del fondo de becas hace casi dos años. En ese momento, también les dije que mis padres tienen un fondo de becas similar para mí. También tengo un fondo secreto del que no te he hablado.
Sara se enojó con Johnny
Sara: ¿Desde cuándo empezamos a tener secretos entre nosotros? Siempre les he contado todo sobre mí: a dónde quiero ir para la universidad, quién la financiará, cómo se conocieron mis padres, sobre mi Nana y todo lo demás. ¿Por qué me guardas secretos? Me voy a casa.
Sara estaba bastante enojada y se fue. Johnny trató de llamarla por teléfono pero ella lo cortó. No sabía por qué Johnny había sido reservado. Por lo general, ella era bastante estable y estaba bien equilibrada, pero no podía aceptar que Johnny le guardara secretos. Ella pensó: “¿Qué más estaba manteniendo en secreto? Si tiene amigas secretas, puede irse al infierno”. Pasaron los días y ella no hablaba con Johnny. Incluso tomó un camino diferente hacia y desde la escuela para no encontrarse con él.
Varios días después, Sara estaba en casa y sonó el timbre. Fue Johnny. Nana lo había dejado entrar. Johnny tenía un papel en la mano.
Johnny: Sara, lo siento. Debería haberte hablado de ello mucho antes. Esto es lo que no te dije.
Sara: ¿Por qué no me lo cuentas? Dice que tienes mucho más dinero que en tu fondo de becas. Entonces, Johnny, ¿crees que habría estado celoso de ti? Estoy muy feliz por ti, pero ¿por qué mantenerlo en secreto de mí?
Johnny: Porque soy estúpido. No entiendo lo que dice.
5% de interés anual compuesto continuamente
Sara: Dice que en el momento de su nacimiento, alguien le dio un regalo de $10,000 que era dinero depositado en un banco que le daría un 5% de interés anual compuesto continuamente hasta que retirara el dinero.
Johnny: Eso es lo que no entiendo “interés compuesto continuamente”. Nunca he escuchado de eso. Por eso me sentí estúpido al hablar contigo sobre eso.
Sara: Ven aquí mi amor.
Sara le dio a Johnny un largo beso y luego dijo: Una vez mi papá me habló de eso. No lo entiendo muy bien, pero lo resolveremos juntos.
Johnny se sintió aliviado de no ser tan tonto después de todo. Aquí había algo que ni siquiera Sara, su ídolo genio de las matemáticas, sabía, y tenía un promedio de calificaciones del 98 %. No estaba solo. Charlaron y se besaron un rato y luego Johnny se fue a casa. A la mañana siguiente, Sara no evitó a Johnny y fueron juntos a la escuela. Sara le dijo a Johnny que había hablado con su papá, quien le había explicado todo. Tomaría un tiempo y podrían hablar de eso después de la escuela. Después de la escuela, Sara fue con Johnny a su casa donde comieron y bebieron un poco de gaseosa, y luego comenzaron a hablar sobre el misterio “continuamente compuesto” de Johnny.
Sara: La forma en que papá me lo explicó incluía algo de álgebra básica y algunas de las cosas de las que hablamos cuando planeábamos nuestra fiesta de graduación.
Jhonny: ¿Qué? ¿A quién invitar de nuestros 100 amigos o quién se sienta al lado de quién?
Expansión binomial
Sara: Ambos, principalmente sobre las combinaciones, pero empecemos con algo que sabes. ¿Cuánto es (a + b)2?
Johnny: Eso es simple: multiplicas a + b por a y por b y luego sumas los dos juntos como
(a + b) x a = a2 +ab, (a + b) x b = ab +b2, Y luego agregarlas para obtener
(a+b) x (a +b) = a2 + 2ab + b2.
Sara: Podemos determinar los coeficientes de los términos a2, ab y b2 considerando diferentes combinaciones de b. Debido a que las combinaciones de b pueden ocurrir con a o con b, hay un total de dos tipos de opciones pero ninguna da a2. Luego, el coeficiente del término a2 se puede escribir como 2C0, que es 2!/(2!0!) o 1. El término ab proviene de una opción: combinación de b con a. Por lo tanto, el coeficiente de ab podría escribirse como 2C1 que es 2!/((2-1)!(2-1)!) o 2/(1 x 1) que es 2. Para el término b2, debe usar b dos veces del total de dos veces y por lo tanto su coeficiente se convierte en 2C2 o 2!/(0!2!) o 1.
Johnny: ¿Por qué perder el tiempo con todo esto, cuando puedo obtener la respuesta como lo hice?
Sara: Johnny chico, estoy haciendo esto para desarrollar un patrón. Ahora, ¿cuál es (a+b)3?
Johnny: Haz lo mismo – multiplica (a+b) con a+b dos veces y obtén la respuesta
o podría hacer esto sabiendo que (a+b)2 = (a2+ 2ab + b2)
(a2+ 2ab + b2) x a = a3 + 2a2b +ab2
(a2+ 2ab + b2) x b = a2b + 2ab2 +b3
Sumando las dos ecuaciones, obtengo
(a+b)3 = a3 + 3a2b + 3 ab2 + b3.
Sara: Es el mismo patrón, 3C0 opciones que es 1 para a3, 3C1 que es 3 para 3a2b, 3C2 que es 3 para ab2 y 3C3 que es uno para b3.
Johnny: Lo entiendo, pero ¿cuál es el problema?
Sara: Ahora que conocemos el patrón, expandamos (a+b)6. Hazlo a tu manera, multiplica 6 veces, seguiré este patrón para obtener la respuesta.
Muy rápidamente Sara escribió:
(a+b)6 = 6C0 a6 + 6C1 a5b +6C2 a4b2 +6C3 a3b3 + 6C4 a2b4 + 6C5 ab5 +6C6b6
= a6 + 6 a5b +15 a4b2 + 20 a3b3 + 15 a2b4 + 6 ab5 + b6.
Johnny luchó por un rato y luego se le ocurrió la misma respuesta, pero luego dijo: “Sara, sé que eres más inteligente que yo, pero ¿qué estás tratando de demostrar?”.
Sara: Sabes que esta tendencia puede continuar, y para que puedas escribir
(a + b)n = nC0an + nC1 a(n-1) b+ nC2 a(n-2) b2 ………..+ nCn-2 a2b(n-2) +nCn-1 abn-1 + nCnbn.
También podrías resumirlo como el Teorema del Binomio
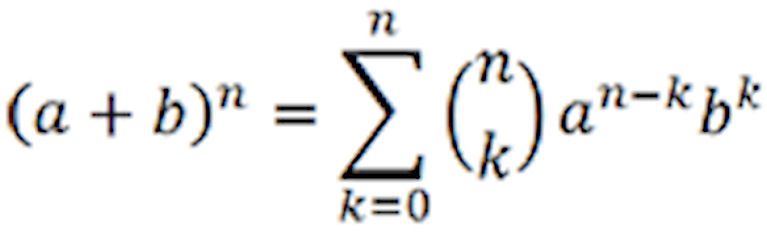
Johnny: Lo entiendo, pero ¿qué tiene esto que ver con mi problema de capitalización continua?
intereses compuestos
Sara: Si decimos que a es el principal y b es igual a la tasa de interés y que la capitalización ocurre n veces, podríamos calcular la cantidad final como (a + b)n.
Johnny: Sí, esa es la idea básica del interés compuesto. Yo sé eso.
Sara: La tasa de interés que se te dará es del 5% anual. Entonces, si alguien fuera a depositar un dólar, al final del primer año tendría $(1+.05) y al final de los dos años, sería $(1 + .05)2. Lo mismo cuando el dinero lleva 20 años en la cuenta. obtendrías la cantidad $(1 + .05)20.
Jhonny: eso lo se Ya calculé que con mi calculadora 1.0520 = 2.6533. Obtendría $26533. No necesitaba tu Teorema del Binomio para eso.
Sara: Entonces, si te digo que obtendrás más dinero, ¿eso te hará feliz o obtendré ese dinero extra?
Johnny: No, no recibes el dinero extra porque el banco lo averiguará y me lo dará si cree que gané más intereses.
Sara: ¿Has escuchado cómo algunos bancos anuncian que te dan una tasa anual del 5% pero la capitalizan mensualmente?
Johnny: Sí, he oído hablar de él. Entonces, el interés mensual sería 0,05 dividido por 12, que es 0,004166667 y el período de tiempo es 20 x 12, que son 240 meses. En ese caso, necesitaría expandir (a + b)n, con a = 1, b = .05/12 o 0.004166667 y n = 240. Wow, eso es mucha capitalización. Uno tendría que hacer muchas multiplicaciones. Veo dónde se podría usar la expansión binomial. Al capitalizarlo mensualmente, me darían $ 10000 x (1.00416667) 240, lo que resulta en $ 27126, que es $ 593 más de lo que pensé que obtendría antes. Sara, la capitalización mensual me dio $593 más.
Sara: Para la capitalización diaria, su interés diario se convertirá en 0,05 dividido por 365, pero se capitalizará 7300 veces. ¿Qué es (1+.05/365)7300.
Johnny estaba emocionado y cambió a su computadora portátil para hacer estos cálculos. El número (1+.05/365)7300 resultó ser 2.7181, lo que significa que con la capitalización diaria obtendría $27181, que era incluso más $27126 que obtendría con la capitalización mensual. Se preguntó si harían capitalización por hora y le preguntó a Sara.
Sara: ¿Por qué detenerse en la capitalización por hora? Digamos si se capitalizaran cada segundo. ¿A quién le importa si no lo hacen? Es divertido pensar cuánto más podría obtener.
Johnny descubrió que el aumento por segundo sería minúsculo (0,05/365/24/3600), pero la capitalización ocurrirá 20 x 365 x 24 veces 3600, que es la friolera de 567 648 000 veces. Así que calculó la cantidad final en $10000 x 2.4596 o $27183, que era solo dos dólares más que la capitalización diaria.
Expansión binomial y constante de Euler
Sara: Verás, incluso si sigues aumentando cada segundo, no obtienes mucho más. Puede seguir acortando el intervalo de capitalización a microsegundos y la capitalización será un millón de veces más frecuente. Verás que el cielo no es el límite para la cantidad de dinero que podrías conseguir. Podríamos escribir 1 en lugar de a y 1/n en lugar de b, entonces

Dado que 1n-k = 1, (1+1/n)n = suma de (nCk (1/n)k) de k =0 an o podría escribir

Cuando n →∞ (1+1/n)n= 1+ 1 + 1/2 +1/6 +1/24 +1/120………………………….
Esta suma se llama el número de Euler o e. No se puede calcular exactamente pero se aproxima a 2.7183. Eso es $ 27183 es aproximadamente el máximo que puede ganar, puede ser unos centavos más si calculamos la serie usando muchos términos.
Johnny: Tengo dos preguntas. Primero, ¿es este el mismo número de Euler del que hablamos cuando estábamos haciendo funciones logarítmicas?
Sara: Sí, los logaritmos naturales son en base e en lugar de 10. ¿Cuál es tu segunda pregunta?
Johnny: Calculamos todo esto durante 20 años. ¿Qué pasa si quiero retirar mi dinero ahora, 18 años después del depósito inicial?
Fórmula de interés compuesto continuo
Sara: El interés compuesto continuo se basa en la fórmula:
A = P ert, donde P es el principal, r es la tasa, digamos 5% o 0,05 por año para usted y t es el tiempo, en este caso el número de años, y es la cantidad final con intereses.
Johnny: Así que con r = 0.05 y t = 18 años, obtendría solo $24596 pero con t = 20 años, obtuve $27183. También calculo que si me retiro después de 50 años, obtendría $121,825.
Sara: Podrías pero tienes suerte de que también discutí esta parte con mi papá.
Johnny: que es eso?
El enigma del impuesto sobre la renta
Sara: Impuesto sobre la renta. En este momento, tienes 18 años y vas a la escuela. Tienes muy pocos otros ingresos de los que hablar. No hay impuesto sobre la renta en pequeños obsequios como este, pero el interés ganado en ellos se considera ingreso imponible.
Johnny: Entonces, si retiro ahora, mi ingreso será de $24 596 menos $10 000, que es $14 596. Me pregunto cuánto tendré que pagar de impuesto sobre la renta.
Sara: Muy poco porque no tienes muchos otros ingresos pero si te retiras después, tendrás ingresos del fondo de becas y luego de tus trabajos. El monto del impuesto sobre la renta seguirá aumentando.
Johnny: Entonces, ¿estás diciendo que debería retirar este dinero ahora?
Sara; Yo no dije eso. Una de las posibilidades es que pueda poner este dinero en una cuenta de ahorro libre de impuestos. Si lo hace, tendrá que pagar impuestos sobre la renta por la cantidad ganada hasta ahora, pero podría seguir ganando más sin pagar intereses.
Johnny: Pero si lo hago ahora, tengo que pagar el impuesto sobre la renta ahora con algún otro dinero.
Sara: Habla con tu papá. Me sorprende que aún no hayas tenido esta charla con él. Estoy seguro de que estará encantado de ayudarte. De esa manera, puedes tener tu pastel y comértelo también.
Johnny: Gracias Sara. Lamento mucho haberte mantenido esto en secreto hasta ahora. Hablaré con mi papá.
Sara: Me imagino que puedes guardar el dinero en la cuenta de ahorro libre de impuestos para retirarlo en el futuro cuando compremos una casa juntos. ¡Es una broma!
Johnny le dijo que era un zorro y le dio un fuerte abrazo y un largo beso.
Desafío
Farah, una estudiante de grado 11, estaba sentada en la cafetería y charlando con sus amigos. Se jactaba de su herencia. Su abuelo le había dejado una herencia de $ 120,000 que se depositó en su décimo cumpleaños, pero ella tendría acceso completo a ella cuando cumpliera 18 años. El monto depositado ha estado ganando una tasa de interés compuesta anual del 5 por ciento. Determina la cantidad en su cumpleaños número 18 usando la expansión binomial.
Solución: La cantidad al final del año n está dada por 120 000 x (1+.05)n porque el interés es del 5% anual compuesto anualmente.
La expansión binomial se puede escribir como la fórmula
(a + b)n = nC0 an + nC1 a(n-1) b + nC2 a(n-2) b2 ………..+ nCn-2 a2b(n-2) +nCn-1 abn-1 + nCn bn
Usando a =1 y n = 8 que es la diferencia entre los años 18 y 10, esta expansión se convierte en
8C0 + 8C1 b + 8C2 b2 + 8C3 b3+ 8C4 b4+ 8C5b5+ 8C6 b6 + 8C7 b7+ 8C8 b8
= 1 + 8 b + 28 b2 +56 b3+ 70 b4+ 56b5+ 28b6 + 8b7+ b8
Con b = 0.05, se convierte en 1. 1.477455. Entonces la cantidad será 120000 x 1. 1.477455 ≈ $177295.