
El Sr. John Power ingresó a su clase de Trigonometría… feliz
El Sr. John Power ingresó a su clase de Trigonometría. Parecía muy feliz. En ese momento, algunos estudiantes sintieron que el Sr. Power estaba tramando algo. Sabían que le gustaba desafiarlos, y el hecho de que fuera feliz significaba que se le había ocurrido uno difícil de descifrar.
Mr. Power se dirigió a la clase: Hoy, en lugar de una lección, tendrán una pregunta interesante que resolver. Para esto, muchos estudiantes pueden trabajar juntos. Estás sentado en tres filas. Cada fila puede formar un grupo. Tienes 20 minutos para resolver el problema.
El problema: determine el valor de π usando su conocimiento de trigonometría.
La mayoría de los estudiantes estaban asombrados. ¿Por qué Mr. Power los torturaría así? No tenían ni idea de cómo abordar el problema porque nunca había hablado de eso en la clase. Todo lo que recordaban eran definiciones de algunas funciones trigonométricas y algunas identidades que habían memorizado. Nunca apareció en ninguna de las hojas de trabajo que hicieron. Simplemente se miraron el uno al otro preguntándose si alguien más iba a dar una respuesta.
Después de que pasaron los 20 minutos, preguntó a los estudiantes de la fila 1, quienes respondieron: Sr. Power, aún no hemos cubierto esto en clase.
De la fila 2, uno de los estudiantes dijo con orgullo: Sabemos que el coseno inverso (también llamado arccos) de -1 es π radianes. Usamos nuestras calculadoras y determinamos el valor de cos inverso de -1 y obtuvimos un valor de 3.14159265359. Entonces π = 3.14159265359.
El Sr. Power estaba frustrado porque esto era casi tan malo como simplemente obtener el valor de π de Internet, pero dijo: “Buen esfuerzo”.
Luego se volvió hacia el tercer grupo y le preguntó a Sara: Espero que a tu grupo le haya ido mejor que eso.
Sara dijo que sí, y él la llamó a la junta para explicarle lo que hacían.
Sara: En realidad, todo fue genialidad de Tommy.
Tommy dijo que tenía hambre y deseaba tener pizza hawaiana. Eso nos dio la gran pista sobre cómo proceder. Tuvimos una breve discusión, pero luego decidimos que un círculo no era más que un polígono de lados infinitos como una pizza gigantesca con muchas porciones. Tommy estaba más preocupado por la piña y los trozos de jamón en la pizza. Simplemente le dijimos que se quedara callado, de lo contrario no obtendría nada.

Para resolver este problema, decidimos comenzar con una pizza de 6 rebanadas (Fig. 7.1). Primero, examinamos una rebanada de pizza. Comenzó desde el centro de la pizza en A. Dibujamos una línea BC para conectar las otras dos esquinas de la rebanada. En lugar de la rebanada, esto nos dio un triángulo ABC. En este momento no nos preocupamos por la pequeña cantidad de comida entre la línea BC y el borde de la pizza. Discutimos, pero decidimos agonizar con eso más tarde.
Dibujamos una línea punteada vertical desde AD. AD se llama la apotema de este hexágono que es algo así como el radio de un círculo. Asumimos que AD = r que es aproximadamente el radio de la pizza.
El ángulo ABC = 360°/6 ya que los ángulos de todas las rebanadas sumarían 360°. El ángulo BAD sería la mitad de este y por lo tanto 30°. Como ABC es un triángulo isósceles, BD = DC. Llamamos BD =L/2 que es la mitad de la longitud de la base BC del triángulo.
Ahora L/2/r = bronceado (BAD) = bronceado 30° = 0,57735.
Área del triángulo ABC = r x L/2 = 0,57735 r2.
Pero la pizza contenía 6 de esos triángulos. Entonces el área del hexágono en la pizza = 6 x 0.57735 r2 = 3.4641 r2. Esto nos dio el valor de π de 3,4641 porque el área de un círculo es 3,4641 r2.
Duplicar el número de porciones de pizza.
Recuerda, nuestra premisa era que se puede pensar en un círculo como un polígono con lados infinitos. Como siguiente paso hacia eso, examinamos una pizza de 12 rebanadas de la misma manera (Fig. 7.2). Pero Tommy no estaba contento porque eso le daría menos pizza por porción. Entonces dijimos que la pizza puede ser más grande pero se puede cortar en 12 rebanadas iguales. Tommy estaba satisfecho. Dibujamos un triángulo que conecta el centro de la pizza y los bordes de las rebanadas de la misma manera que para la pizza de 6 rebanadas. También dibujamos una línea vertical similar desde A.
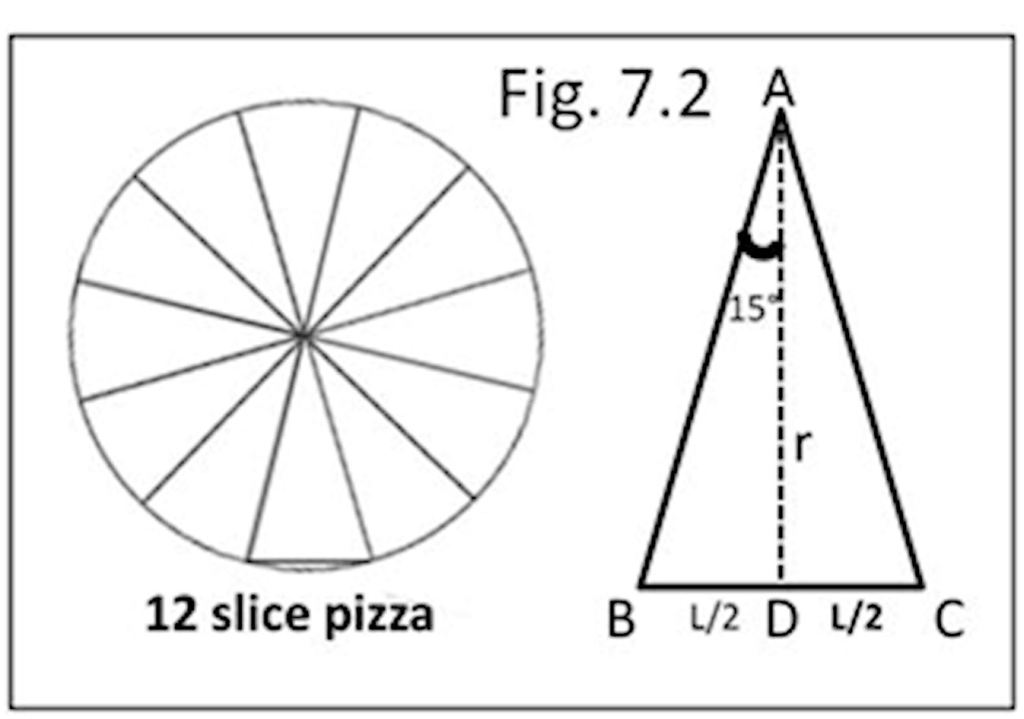
Aquí BD/AD = L/2/r = tan (360/12 x 2) = tan 15°= 0.26795.
Por lo tanto, el área del triángulo ABC
= 0,26795 r2.
El área del dodecágono en la pizza.
= 12 x 0,26795 r2 = 3,2154 r2.
Esto nos dio el valor de π de 3,2154, que es algo menor que 3,4641, que era el valor que habíamos obtenido de la pizza de 6 porciones.
Nos dimos cuenta de que la determinación del valor de π de los polígonos en las pizzas de 6 y 12 rebanadas seguía la misma ecuación. El área del triángulo ABC = tan (360°/2n) x r2 y el área del polígono = n tan (360°/2n) x r2 donde n es el número de lados.
pizza de 100 rebanadas
Luego pensamos en una pizza de 100 rebanadas. A Tommy no le gustó la idea nuevamente porque cada porción sería demasiado pequeña y se quedaría con hambre. Entonces, le dijimos que no se preocupara porque esta pizza sería muy grande como el tamaño de nuestro salón de clases.
Con la misma ecuación, el área de un polígono de 100 lados en la pizza sería:
100 x bronceado (360°/200) x r2 = 100 x 0,03142626604 r2 = 3,142626604 r2. Nuevamente, este valor fue ligeramente menor que los dos valores que habíamos obtenido antes.
Para un polígono de 10 000 lados, el área sería 10 000 x 0,00031415927 r2 = 3,1415927 r2. Aquí están los valores que obtuvimos para las áreas de las diferentes pizzas: 3.4641 r2 (6 rebanadas), 3.2154 r2 (12 rebanadas), 3.142626604 r2 (100 rebanadas), 3.1415927 r2 (10000 rebanadas). Podríamos haber seguido, pero se habían acabado los 20 minutos.
Debido a que el área de Área de un círculo = r2 y el área de un polígono de 10,000 es 3.1415927 r2, obtuvimos π = 3.1415927 aproximadamente.
Mr Power estaba encantado con la respuesta.
Le dijo a la clase que esto era brillante pero no la única manera. Continuó diciendo que aunque habían comenzado a aprender Trig usando triángulos de ángulo recto, ahora deberían saber que Trig se puede usar para cualquier triángulo y polígono. También deben explorar cómo Trig también se puede usar para cualquier cuadrilátero y poliedro. Les dio varios problemas del libro Trigonometría como tarea.
Johnny, por ahora. le gustaban las cosas asombrosas que podía hacer con Trigonometría gracias a la ayuda de la novia que amaba. Escribió el examen final con confianza. De hecho, obtuvo un 99% total en el curso. Esta nota le ayudó a conservar la bicicleta porque su promedio general de todos los recorridos estuvo muy por encima del 85 %. Sara le contó esta historia a su Nana (abuela) a quien amaba mucho. Nana dijo: “No me sorprende porque eres Sarasvati, la diosa del conocimiento. Sara es solo tu apodo”.
Desafío
Johnny entra en una carrera de bicicletas. Sara le pregunta: “¿Cuánto dura la carrera?” Johnny: “No lo sé, pero según este mapa, desde el punto de partida recorremos 20 km por una carretera que va hacia el oeste, después de lo cual el camino norte – este toma un ángulo de 70°. Recorremos 18 kilómetros por esta vía y luego giramos hacia otra vía Este con un ángulo de 110° y recorremos 15 kilómetros. Después de eso, tomamos un camino que nos lleva de regreso directamente a nuestro punto de partida”. Sara dice: “Entonces, la ruta es un trapezoide”. ¿Cuánto tiempo calculaste que sería la carrera en bicicleta?
Solución: Dibujamos un cuadrilátero ABCD (Fig. 10.6). Dado: AB = 20 km, BC = 18 km, CD = 15 km, ángulo ABC = 70°, ángulo BCD = 110°. Dado que la suma de los ángulos ABC y BCD = 180°, las líneas AB y CD deben ser paralelas, por lo que el cuadrilátero es un trapezoide. Necesitamos la suma de los cuatro lados para obtener la distancia para la ruta en bicicleta. Se dan las longitudes de AB, BC y CD, pero necesitamos determinar la longitud de DA para resolver este problema.

Trazamos dos líneas verticales: CE de C a AB y AF de A a CD.
En el triángulo EBC, ángulo EBC = ángulo ABC = 70°.
Por lo tanto, CE/BC = sin 70° o CE = BC sin 70° = 18 x 0,9397 = 16,9146 km.
BE/BC = cos 70° o BE = BC cos 70° = 18 x 0,342 = 6,156 km.
AE = AB – BE = 20 – 6,156 = 13,844 km.
Debido a que AB y CD son paralelos, CE y AF siendo perpendiculares a ellos también deben ser paralelos.
Por lo tanto AF = CE = 16,9146 km.
y CF = EA = 13,844 km.
Porque se nos da que CD = 15 km, FD =15 – 13,844 = 1,156 km.
Debido a que AF se dibujó como una línea perpendicular a CD, el triángulo AFD es un triángulo de ángulo recto. Del teorema de Pitágoras
DA2 = AF2 + FD2 = 13,8442 + 1,1562 = 192,993 o DA = 13,892 km.
Por lo tanto, la distancia total de la ruta en bicicleta = 20 + 18 +15 + 13.892 = 66.892 km.